今天为大家介绍的是来自伦敦Google DeepMind的David Pfau团队的一篇论文。作者提出了一种通过变分蒙特卡罗方法估算量子系统激发态的算法，该算法没有自由参数，也不需要对状态进行正交化，而是将问题转化为寻找扩展系统基态的问题。该方法可以计算任意可观测量，包括诸如跃迁偶极矩等非对角期望值。这种方法在与神经网络波函数相结合时表现得特别好，通过将该方法与FermiNet和Psiformer波函数结合，作者可以精确地恢复一系列分子的激发能和振子强度。包括具有挑战性的双重激发在内，作者在苯尺度上的分子上实现了精确的垂直激发能。除了本文中展示的例子之外，作者预计该技术将对原子物理、核物理和凝聚态物理产生积极影响。

理解物质与光相互作用的物理原理需要对量子系统的电子激发态进行精确建模。这是光催化剂、荧光染料、量子点、发光二极管(LED)、激光器、太阳能电池等行为的基础。现有的量子化学方法在处理激发态时，精确度往往远低于对基态的处理，有时甚至会在质量上出现问题，或者需要针对特定状态的先验知识。神经网络结合变分蒙特卡罗(VMC)方法，已经在一系列系统中（包括自旋模型、分子和凝聚态系统）的基态波函数计算中达到了显著的精确度。尽管VMC已被用于研究激发态，但现有方法的局限性使得它们难以与神经网络结合使用，且通常有许多自由参数需要调整以获得良好的结果。

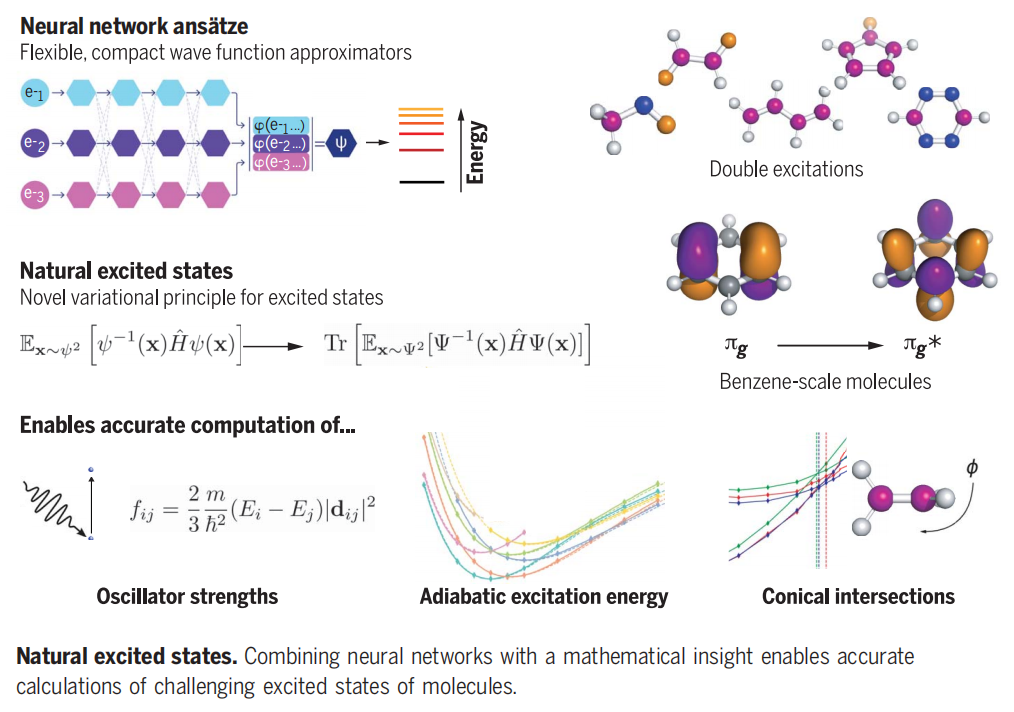
作者将神经网络波函数（ansätze）的灵活性与一种数学洞见相结合，这能够将寻找系统激发态的问题转化为寻找扩展系统基态的问题，然后可以使用标准的变分蒙特卡罗方法（VMC）来解决。作者称这种方法为自然激发态VMC（NES-VMC）。激发态的线性独立性通过波函数形式自动实现。每个激发态的能量和其他可观测量是通过对单态波函数上哈密顿期望值矩阵的对角化来获得的，这可以在不增加额外成本的情况下进行积累。关键的是，这种方法没有需要调整的自由参数，也不需要通过惩罚项来强制正交化。作者使用了两种不同的神经网络架构——FermiNet和Psiformer，来检验该方法的准确性。

作者在从单个原子到苯大小的分子等基准系统上展示了该方法的优越性能。

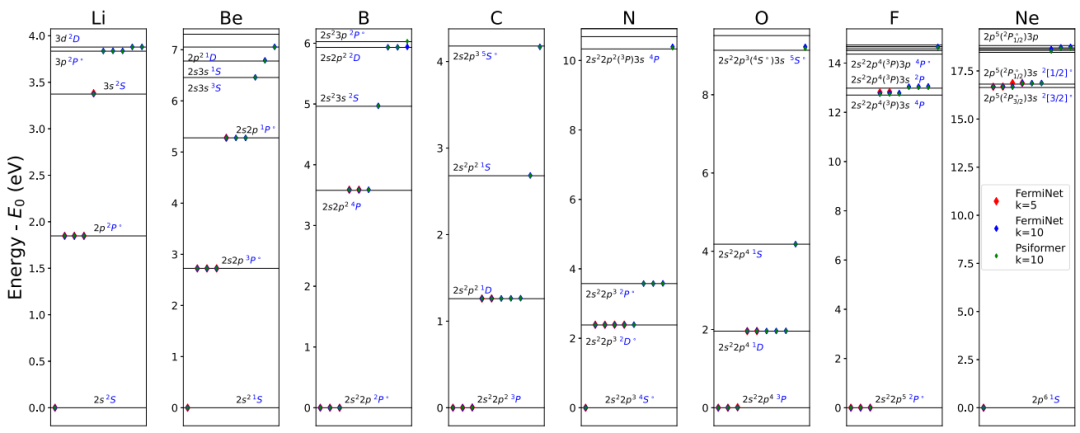
图 1

如图1所示，为了研究波函数选择以及计算状态数k的影响，作者使用FermiNet进行了包含5个和10个状态的计算，并使用Psiformer进行了包含10个状态的计算。

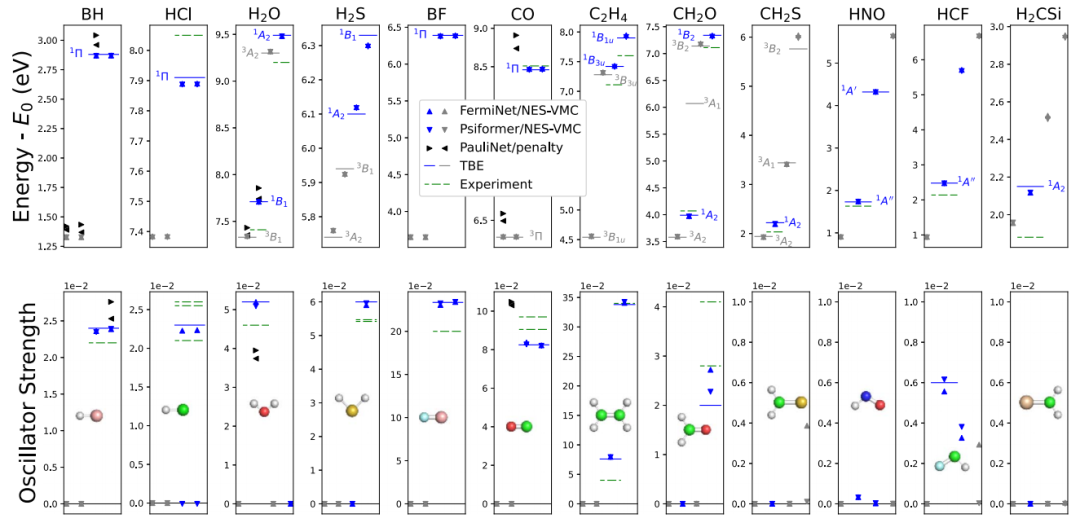
图 2

在图2中，作者将NES-VMC应用于Chrayteh等人研究的所有小分子，使用FermiNet和Psiformer计算了五个最低能量状态以及所有跃迁的振子强度。作者验证了NES-VMC在第一周期元素原子上的准确性，结果与实验结果非常接近，并在一系列小分子上获得了与现有最佳理论估计相当的高精度能量和振子强度。

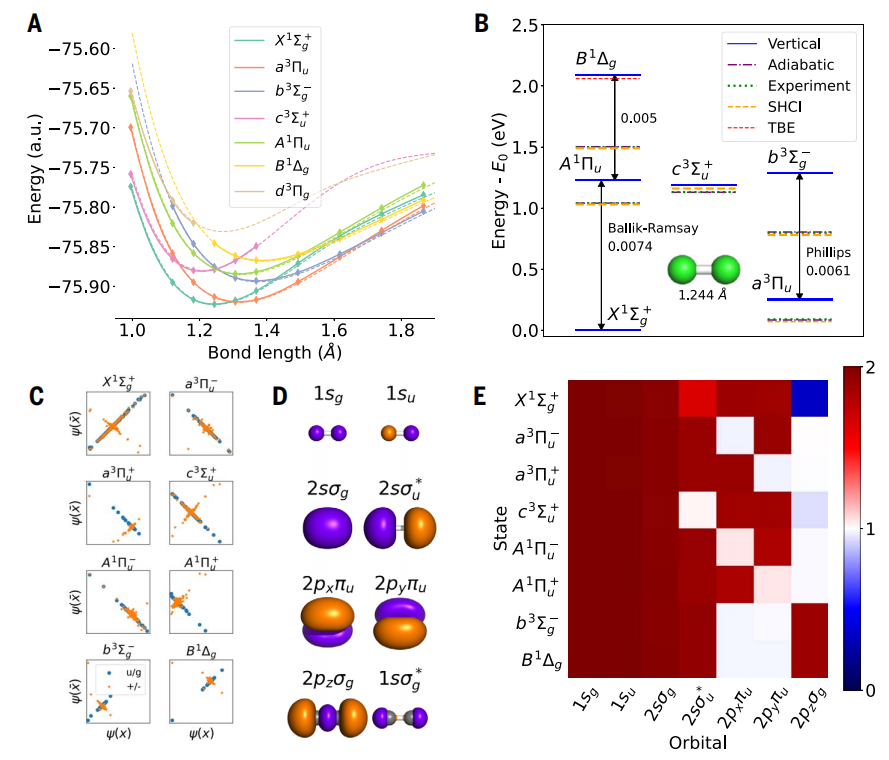
图 3

如图3所示，作者使用Psiformer波函数计算了碳二聚体最低激发态的势能曲线，并通过分析它们的对称性和自旋来识别不同键长下的状态。NES-VMC的垂直激发能与高度精确的半随机热浴配置相互作用（SHCI）方法在所有键长上的结果保持在化学精度范围内，而绝热激发能与实验值的平均差距仅为4 meV，比SHCI方法提高了四倍。

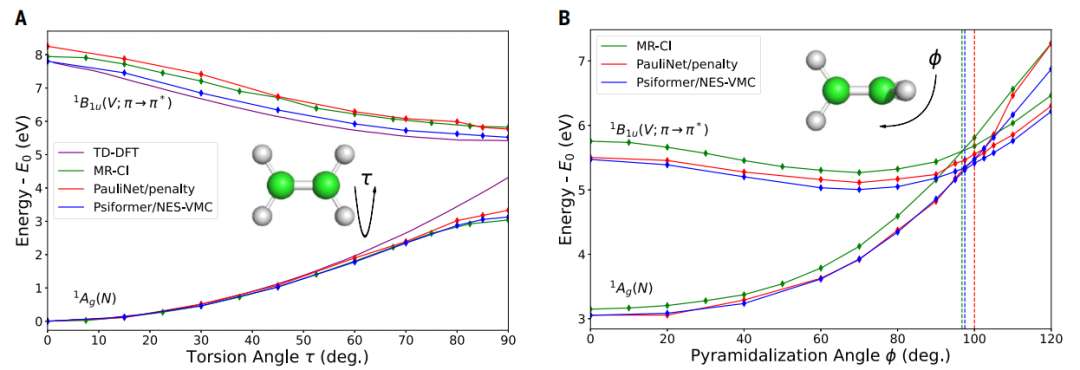
图 4

作者计算了乙烯在扭转角从0°到90°变化时的激发态，然后锥体化角从0°到120°的变化，足以包括N态和V态的锥形交点。图4中的结果显示，NES-VMC正确描述了扭曲分子的锥形交叉，并与高度精确的多参考配置相互作用（MR-CI）结果高度一致。

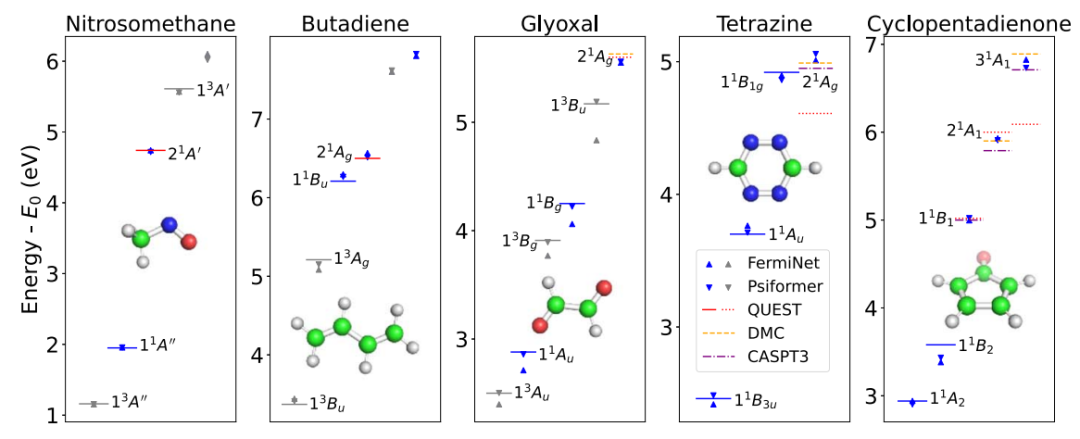
图 5

在图5中，作者还研究了五个具有低能双重激发的包括多个苯尺度分子在内的挑战性系统。在所有方法对垂直激发能具有良好一致性的系统中，Psiformer在所有状态下都达到了最优化学精度。在四嗪和环戊二酮中，几年前被认为不准确的最先进计算结果与NES-VMC的结果与最近的复杂扩散蒙特卡罗（DMC）和完全活性空间三阶微扰理论（CASPT3）计算结果高度一致。

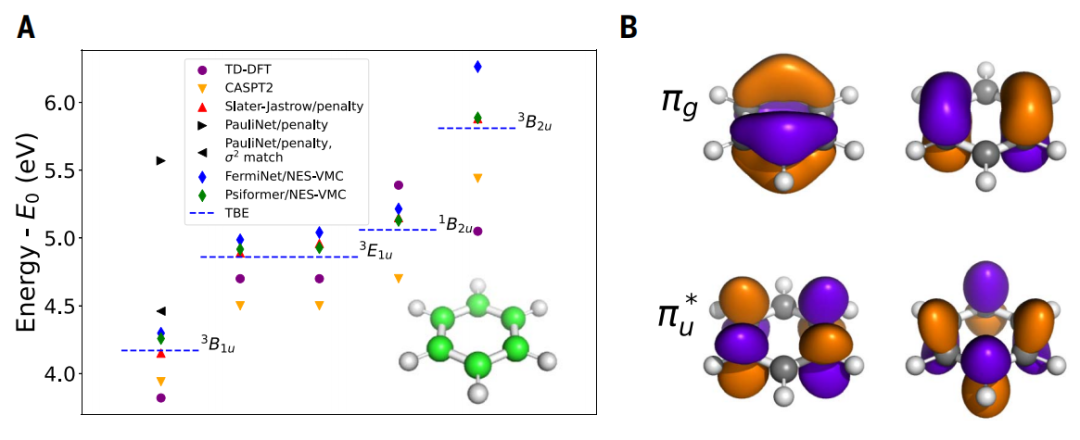
图 6

最后，作者研究了苯分子，图6中的NES-VMC结合Psiformer波函数与理论最佳估计相比，表现出显著更好的一致性，超越了包括使用罚项方法的神经网络波函数。这不仅验证了作者方法在数学上的正确性，也表明神经网络可以在当前计算方法的极限下准确表示分子的激发态。

NES-VMC是一种无参数且数学上严谨的激发态变分算法。通过将其与神经网络波函数相结合，可以在广泛的基准问题上实现显著的精度。对量子系统激发态的精确VMC方法的发展打开了许多可能性，并极大地扩展了神经网络波函数的应用范围。尽管作者只考虑了分子系统的电子激发和神经网络波函数，但NES-VMC适用于任何量子哈密顿量和任意波函数，这使得能够进行精确的计算研究，从而提高我们对振动耦合、光学带隙、核物理以及其他具有挑战性问题的理解。

编译 | 于洲

审稿 | 曾全晨

Pfau D, Axelrod S, Sutterud H, et al. Accurate computation of quantum excited states with neural networks[J]. Science, 2024, 385(6711): eadn0137.