Published on October 24, 2025 6:32 PM GMT
TLDR: Anthropic's recent paper "When Models Manipulate Manifolds" proves that there are meaningful insights in the geometries of LLM activation space. This matches my intuition on the direction of interpretability research, and I think AI safety researchers should build tools to uncover more geometric insights. This paper is a big deal for interpretability research because it shows that these insights exist. Most importantly, it demonstrates the importance of creating unsupervised tools for detecting complex geometric structures that SAEs alone cannot reveal.
Background
Interpretability researchers have long acknowledged the limitations of sparse autoencoders, including their failure to capture more complex underlying structure. See:
- Deepmind's blog post from earlier this year.Anthropic's list of SAE/transcoder/crosscoder/attribution graph limitations.
SAEs are useful but can only provide a limited view into LLM behavior, but they fail to capture more complex structures within an LLM, if they exist. Fundamental insights require a more granular view. Meanwhile, there is strong empirical and theoretical evidence supporting the idea that there are insights in the activation space of LLMs that more geometric approaches might uncover:
- Superposition and Polysemanticity: Anthropic posed the idea that if models store more features than they have dimensions, then there will be some interference between features. One would conclude that we would see interesting failure modes when this interference reaches a critical mass, and we do. Researchers showed that hallucinations are byproducts of information compression in LLMs.
- Goodfire's recent paper on adversarial examples corroborates this, demonstrating adversarial attacks are a byproduct of polysemanticity.
All this suggests that there are underlying structures or processes for LLMs to store information and higher-level/abstract concepts in ways that are entangled with each other. With the right analysis, we could peer into the black box of LLMs in ways we have not before.
- The natural conclusion to this thinking is the Manifold Hypothesis. This theory claims that neural networks learn to operate in high-dimensional space by learning the low-dimensional manifolds of their training data. While I'm not convinced this is an accurate description of what's happening, it I do think it points us towards a more productive path of research. My intuition for the past year was that SAEs were giving us too flat a representation; they only show us 1D fragments of complex, higher-dimensional structures. Maybe simpler datasets existed on low dimensional manifolds, but human text is enormously more complex.
What's a manifold?
A manifold is an abstract concept of some space (not necessarily a subset of Rn euclidean space) that has subsets that looks like Rn, and admits a series of charts which can map regions of the manifold to Rn.
The best place is to start with something we know. Think about the world. It's a sphere. Us humans use flat, 2d, paper maps to navigate the world (the surface of a 3D sphere). The problem is that a sphere's surface cannot be accurately projected onto 2D space without breaking some fundamental concept of geometry. Think about the Mercator projection distorting area to preserve angles for navigation.
The surface of a 3D sphere is a good example of a manifold. Its some abstract space, which in a small radius (like O(~50 miles)) can easily be represented (and mapped to with a homeomorphic function) as a flat, 2D space using x,y coordinates. Any function that operates over this arbitrary radius can be thought of (and analyzed with calculus) as a function like z=f(x,y). All you would need to do is properly map from the manifold to a subset of euclidean space.
We call a function which can turn some arbitrary area in a manifold into a local, Euclidean space a chart, keeping with the cartography analogy. If the entire manifold can be completely represented with a series of charts, then all of the charts are collectively called an atlas. Euclidean space Rn is also a manifold with this definition.
A sphere requires multiple charts, which is why a perfect world map that does not distort any information is impossible. Different manifolds will have different qualities and assurances. A Smooth manifold, for example, requires that when moving between overlapping chart functions, those transitions are smooth (infinitely differentiable). A Riemannian Manifold builds on that and requires that a valid notion of inner products and distance exist. I only add these two examples because I wanted to show that at its core, a manifold strips away and abstracts all assumptions we tend to make about "space."
- We know that LLMs store ideas as directions, and pushing in certain directions can induce certain, predictable behaviors (RepE).We know that LLM information compression is a noisy process with interference (superposition/polysemanticity), and we later found out that this noisiness/overlap can provide a more mathematical explanation for hallucinations, failures modes, and adversarial examples.
This is strong, but not yet conclusive, evidence that we could gain more insight into LLM behavior by taking a more geometric approach. Of course, at this point this is all mostly vibes, without any useful or actionable insight. But because I had this intuition, I’ve spent the past few months trying to strengthen my mathematical toolkit to turn this intuition towards something more concrete.
When Models Manipulate Manifolds
The paper released by Anthropic a few days ago partially validates this thinking, and I think it is a much bigger deal for the interpretability community than its relative obscurity implies. It's also a monster of a paper, but there are multiple fascinating and actionable insights sprinkled throughout. To summarize their findings:
- They attempt to understand how Claude 3.5 Haiku performs a line break task, inserting a new line token before a line of text exceeds a certain character length bound.
- They break this task down into a few steps that the model completes: estimating current line character count, calculating the remaining characters in a line, then using the next planned word to determine if it fits in the current line.
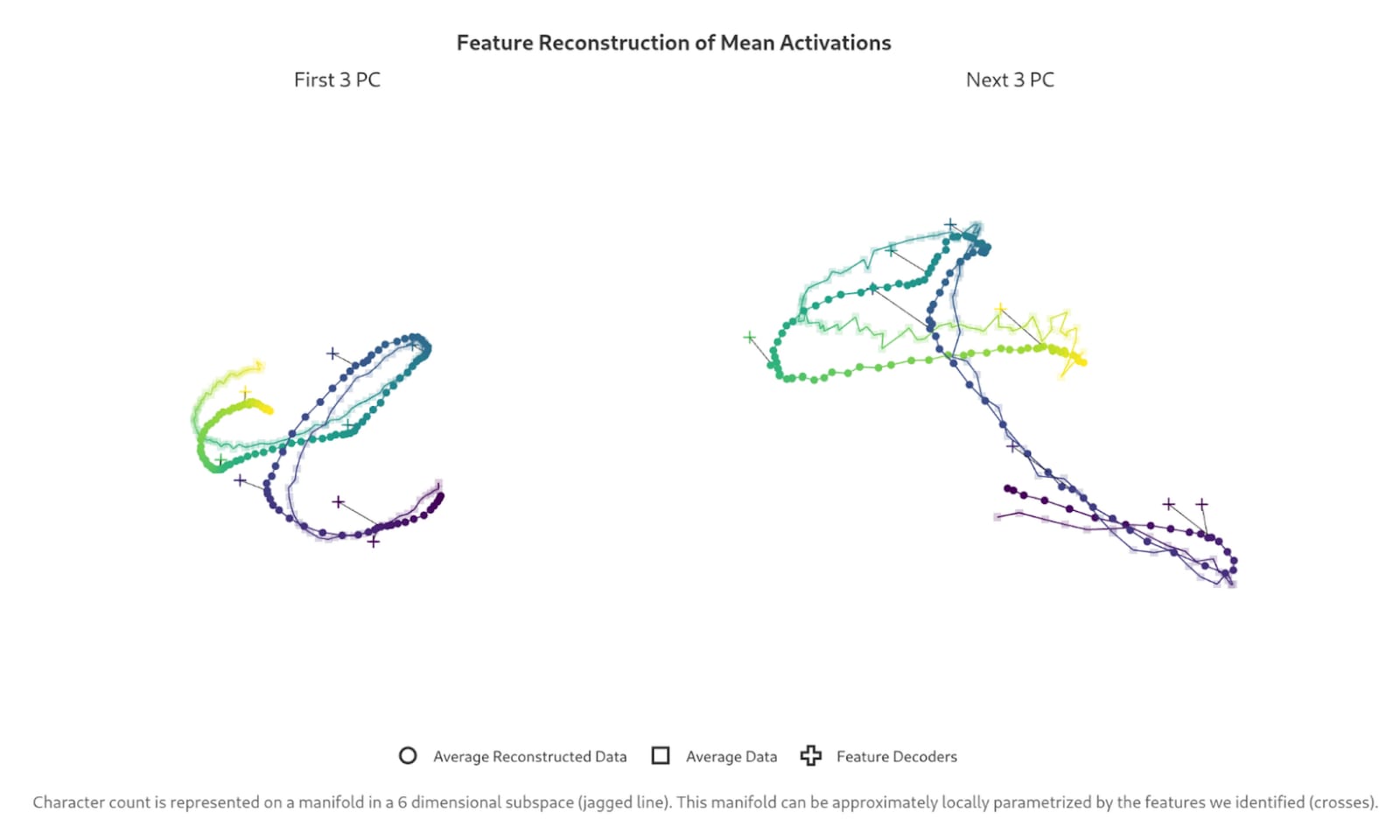
- More specifically, they find a set of features in the residual stream correlating with line character length, and then take the top-6 principal components, with 1st, 2nd, and 3rd Principal Components showing a clean helix and the 4th, 5th, and 6th showing a scrappier one.
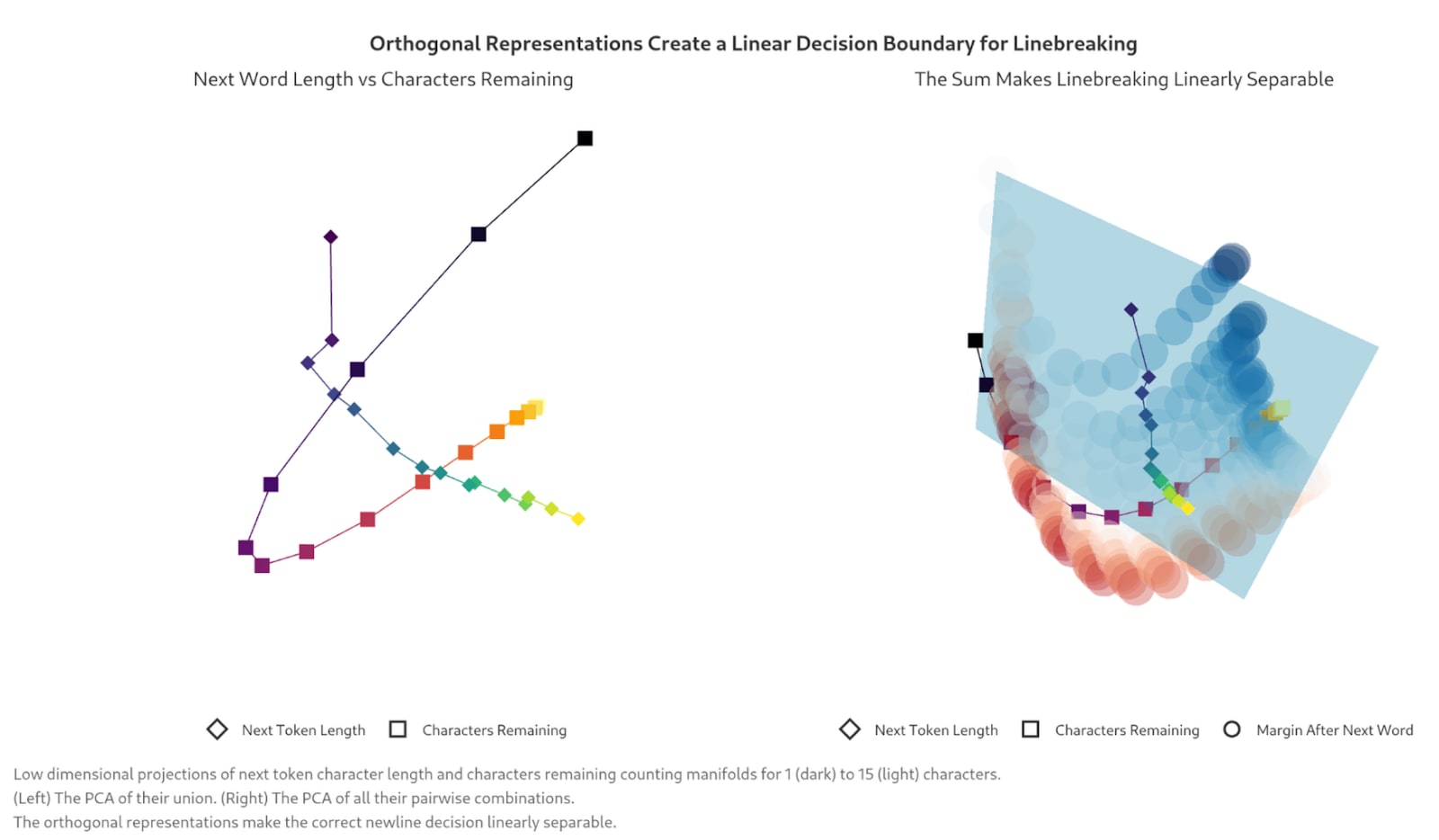
- The model's attention heads manipulate the character count such that when the count is close to the max line length, the new line is strongly attended to.Multiple attention heads compose to produce a notion for "characters remaining." Ablation and intervention confirm the importance of this calculation.The higher dimension representation of current line width and maximum line width enable the model to know when it should insert a line break in ways a lower dimensional representation would not allow.
- The geometric representation allows the model to build a simple decision boundary between characters left on a line and the length of a possible token. The researchers find that using this decision boundary model on real data inserts a new line with high accuracy.
Why This Matters
The most important takeaways from this paper appear in Anthropic’s call-to-action towards the end of the paper (italics added by me):
Complexity Tax. While unsupervised discovery is a victory in and of itself, dictionary features fragment the model into a multitude of small pieces and interactions – a kind of complexity tax on the interpretation. In cases where a manifold parameterization exists, we can think of the geometric description as reducing this tax. In other cases, we will need additional tools to reduce the interpretation burden, like hierarchical representations or macroscopic structure in the global weights. We would be excited to see methods that extend the dictionary learning paradigm to unsupervised discovery of other kinds of geometric structures.
A Call for Methodology. Armed with our feature understanding, we were able to directly search for the relevant geometric structures. This was an existence proof more than a general recipe, and we need methods that can automatically surface simpler structures to pay down the complexity tax. In our setting, this meant studying feature manifolds, and it would be nice to see unsupervised approaches to detecting them. In other cases we will need yet other tools to reduce the interpretation burden, like finding hierarchical representations or macroscopic structure in the global weights.
This vein of research is hinting at something that could enable us to better understand why LLMs do things, and Anthropic is now calling us to take a closer look. We’re seeing strong evidence that there should be insight to gain, and now we’ve seen a concrete example of geometric structures explaining specific behaviors. I think it would benefit the AI safety community and mech interp researchers to work on creating unsupervised tools for detecting complex geometric structures that SAEs cannot. I think this paper offers the most valuable research opportunity for LLM interpretability, and I don’t think enough people in the AI Safety community are acknowledging it yet.
Discuss