💡 **eNTK作为可解释性工具**：经验神经切线核（eNTK）被提出作为一种潜在的工具，用于理解神经网络学习到的特征。研究通过在具有已知真实特征的玩具模型中进行实验，来检验eNTK是否能帮助发现这些特征。

⛰️ **特征谱的“悬崖”现象**：在超分辨（Superposition）玩具模型和模运算MLP（Modular Arithmetic MLP）模型中，eNTK的特征谱（eigenspectrum）表现出明显的“悬崖”现象。这些尖锐的下降点与模型能够识别和学习到的真实特征的数量高度相关。

🚀 **eNTK与“Grokking”相变**：在模运算MLP模型中，eNTK谱的演变过程与“grokking”相变（一种模型在训练后期突然从低准确率跃升至高准确率的现象）的发生时间点同步。这表明eNTK可以作为检测模型内部相变的一个指标。

🤝 **eNTK特征与真实特征的对齐**：研究发现，eNTK的顶层特征向量（top eigenspaces）在经过适当的重缩放后，能够与这些玩具模型中的真实特征（ground-truth features）很好地对齐。这在稀疏和密集两种情况下都得到了验证，为eNTK在特征发现方面的实用性提供了证据。

Published on October 16, 2025 6:04 PM GMT

Summary

Kernel regression with the empirical neural tangent kernel (eNTK) gives a closed-form approximation to the function learned by a neural network in parts of the model space. We provide evidence that the eNTK can be used to find features in toy models for interpretability. We show that in Toy Models of Superposition and a MLP trained on modular arithmetic, the eNTK eigenspectrum exhibits sharp cliffs whose top eigenspaces align with the ground-truth features. Moreover, in the modular arithmetic experiment, the evolution of the eNTK spectrum can be used to track the grokking phase transition. These results suggest that eNTK analysis may provide a new practical handle for feature discovery and for detecting phase changes in small models.

See here for the paper: "Feature Identification via the Empirical NTK".

Research done as part of the PIBBSS affiliate program, specifically the call for collaboration to use ideas from renormalization for interpretability. 

Background

In interpretability, we would like to understand how neural networks represent learned features, “carving the model at its joints". Operationally, we would like to find functions of a model’s activations and weights that detect the presence or absence of a feature with high sensitivity and specificity. However, it’s a priori unclear how to “guess” a good candidate answer. ^[1]

One strategy is to look to theories of deep learning. If there existed a hypothetical complete theory that allowed us to “reverse-compile” any model into human-interpretable code, it would (by definition) solve this problem by telling us which effective features a model uses and how they interact to produce the input-output map. Instead of a complete theory however, in 2025 we have several nascent theories that each explain some modest aspects of what some models may be doing, in some corners of the parameter space. ^[2]

Among such theories, the neural tangent kernel (NTK) and its cousins are unique in giving us a closed-form formula for the function learned by a neural network in a specific regime. Namely, one can prove that when models are much wider than they are deep, with weights initialized with a 1/$\sqrt{width}$ scaling, they approximately learn the function

$f^{}i\left(x\right)={\sum }_{{\alpha }_1,{\alpha }_2}{K}^{}ij$(xα1,xα2)yk,α2    (1)

at the end of training, where the index $i$ runs over output neurons (labels of the dataset),  $\alpha$ runs over points in the training set, and the kernel

$K^{}ij(x_1,x_2)={\sum }_{\mu }\frac{d{f}^{}i}{\left(}d{W}_{\mu }$dfj(x2)dWμ ,  (2)

evaluated at initialization, is the eponymous NTK. See earlier posts (1, 2, 3) on Lesswrong for the derivation of (1) and related discussions.

Realistic models are usually not in this regime. However, it’s been conjectured and empirically checked in some cases - although we don't yet know in general when the conjecture is and isn't true - that Eq. (1) with the NTK (2) evaluated instead at the end of training can at times be a good approximation to the function learned by a neural network beyond the theoretically controllable limit.^[3] This conjecture is called the empirical NTK hypothesis, and the NTK evaluated at the end of training is called the empirical NTK (eNTK).

In this post, we will take the eNTK hypothesis seriously and see if the eNTK can be used to uncover interesting structures for interpretability. Concretely, we test if the top eigenvectors of the eNTK align with ground-truth features in a selection of common toy benchmarks where the ground-truth features are known. And the punchline of the post is that this idea more or less works: up to modest rotations that we explain below, we find that the top eigenvectors of the eNTK align with ground-truth features in toy models where the ground-truth features are known.

To compute if a length-$N$ eNTK eigenvector for $N$ the dataset size aligns with a ground-truth feature, we can take the absolute value of its cosine similarity with a length-$N$ "feature vector" whose entries consist of that feature's activation on each data point.  This gives a scalar for each (eigenvector, feature) pair. To visualize how the eigenvectors across a NTK feature subspace align with a selection of features, we will render heatmaps that show this correlation across all pairs.

Results 

In this section, I'll assume familiarity with the toy models being discussed. Their architectures and experiment details are reviewed in the paper.

Toy models of Superposition

In "Toy Models of Superposition," we find that for models with $n=50$ ground-truth features and importance hyperparameter $I=0.8$, across varying sizes of the hidden layer $m$ and values of the sparsity hyperparameter $S$, the (flattened ^[4]) eNTK eigenspectrum contains two cliffs that track (1) the number of features the model is able to reconstruct and (2) the total number of ground-truth features.

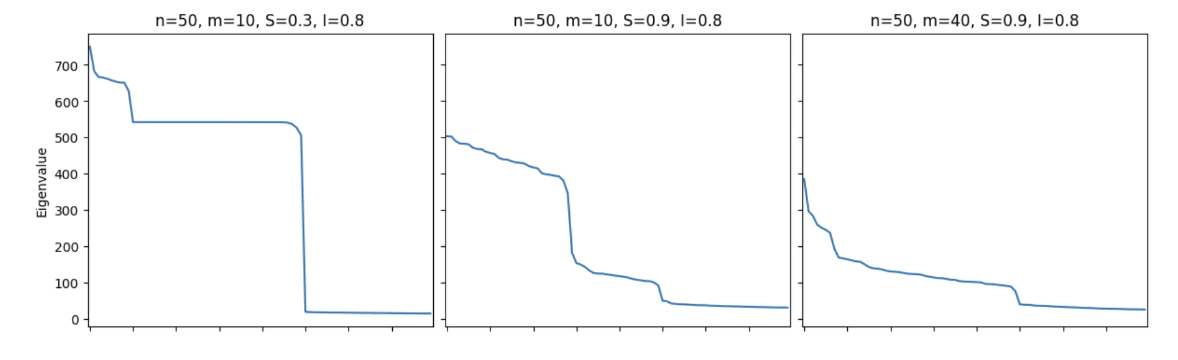
Moreover, upon computing cosine similarity of eNTK eigenvectors in the cliffs with ground-truth feature vectors as described above, we find that the top eNTK eigenvectors align (after an importance rescaling ^[5]) with the ground-truth features in both the sparse and dense regimes. 

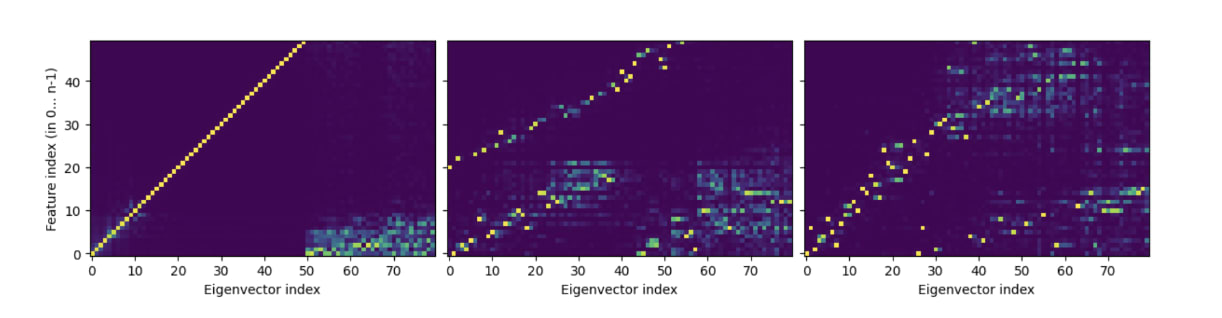
Modular arithmetic

Next, we study a 1L MLP with $n$ hidden neurons, trained to map pairs of one-hot-encoded integers to their one-hot-encoded sum mod $p$ ^[6]. Such models exhibit grokking over a wide range of hyperparameters, suddenly jumping from 0% to 100% accuracy on a held-out test set long after reaching 100% accuracy on the training set. Moreover, we know exactly how these models implement modular arithmetic after the grokking phase transition: by implementing a modular delta function in Fourier space.

Specializing to the hyperparameters $p=29$ and $n=512$ (although we checked that other values give qualitatively similar results), we find that the eNTK spectrum of this model contains two cliffs, each of dimension $4\lfloor \frac{p}{2}\rfloor =56$. This is the right counting for each cliff to contain two sets of Fourier feature families ^[7]. 

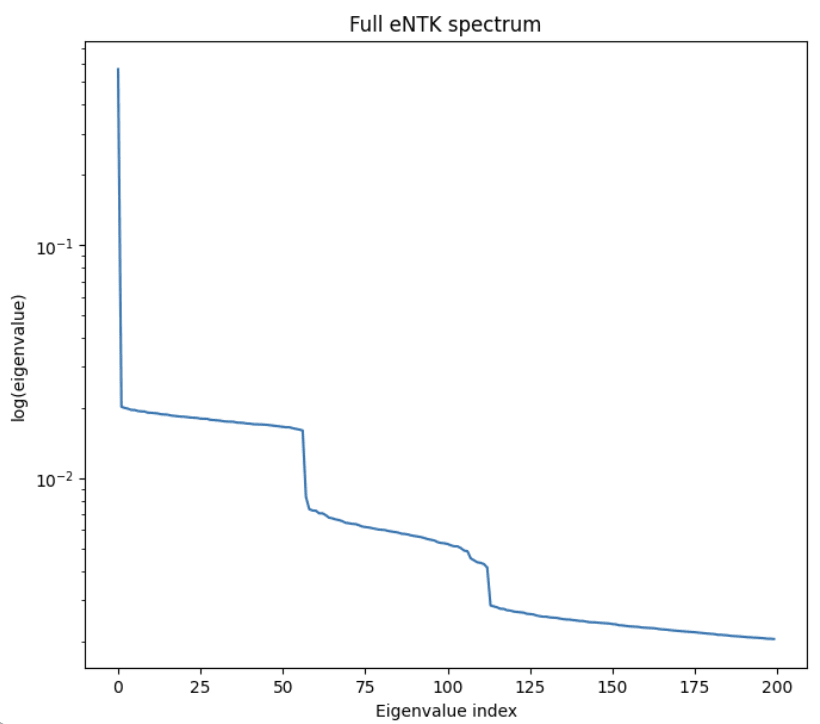
Looking at the time evolution of the spectrum, we find that the first cliff already exists at initialization (!) - suggesting that we could perhaps have predicted the use of Fourier features at initialization using the eNTK - while the second appears at the same time as the grokking phase transition. ^[8]

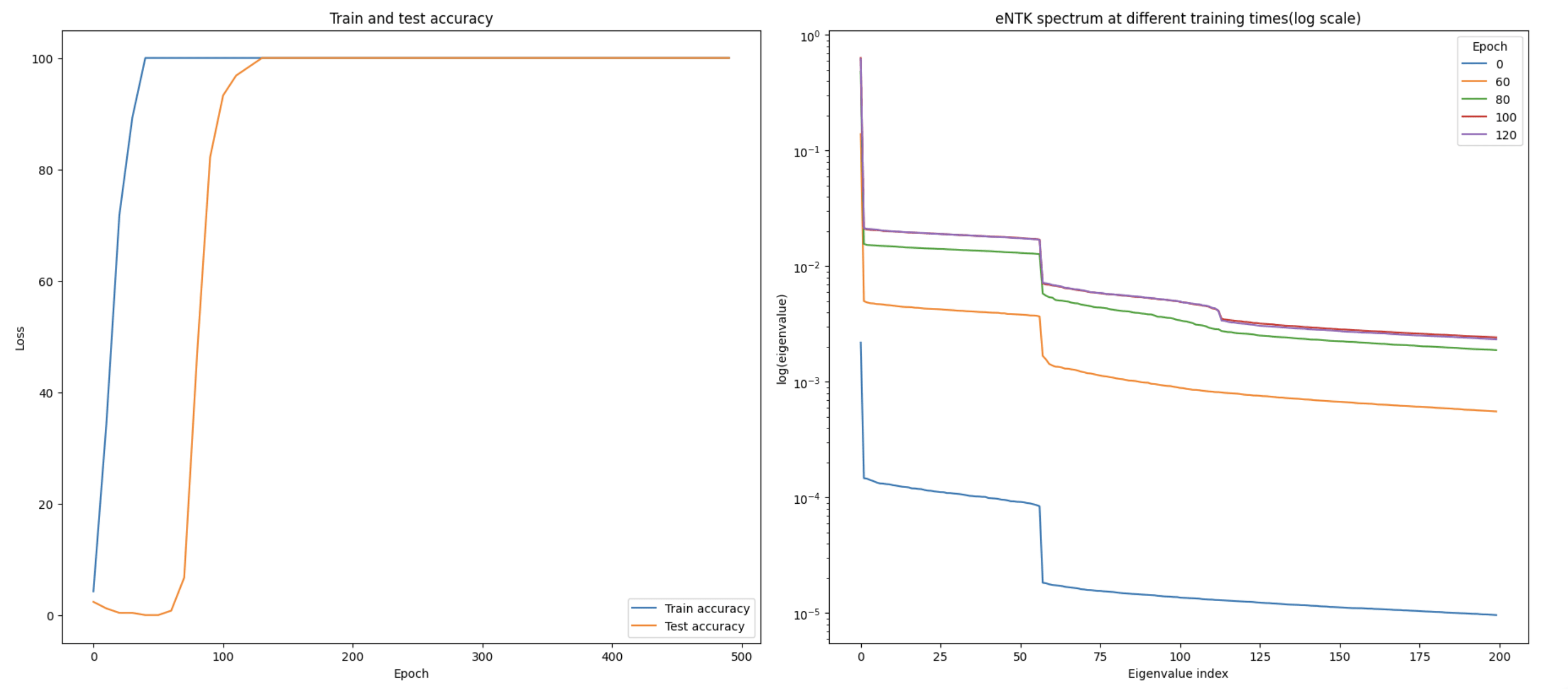
Moreover, we show that beyond having the correct counting, the eNTK eigenvectors in each cliff specifically coincide with a pair of Fourier feature families.  In the paper, we show that a rotation of the eigenvectors in each cliff motivated by symmetries of the dataset causes the eigenvectors in the first cliff to line up with the '$a$' and '$b$' Fourier feature families, and those in the second cliff to line up with '$a+b$' (sum) and '$a-b$' (difference) Fourier feature families, for $(a,b)$ the two inputs to the arithmetic problem.

The following heat maps show the cosine similarity between the rotated eNTK eigenvectors in the second cliff and feature vectors for the sum and difference Fourier families at different epochs:

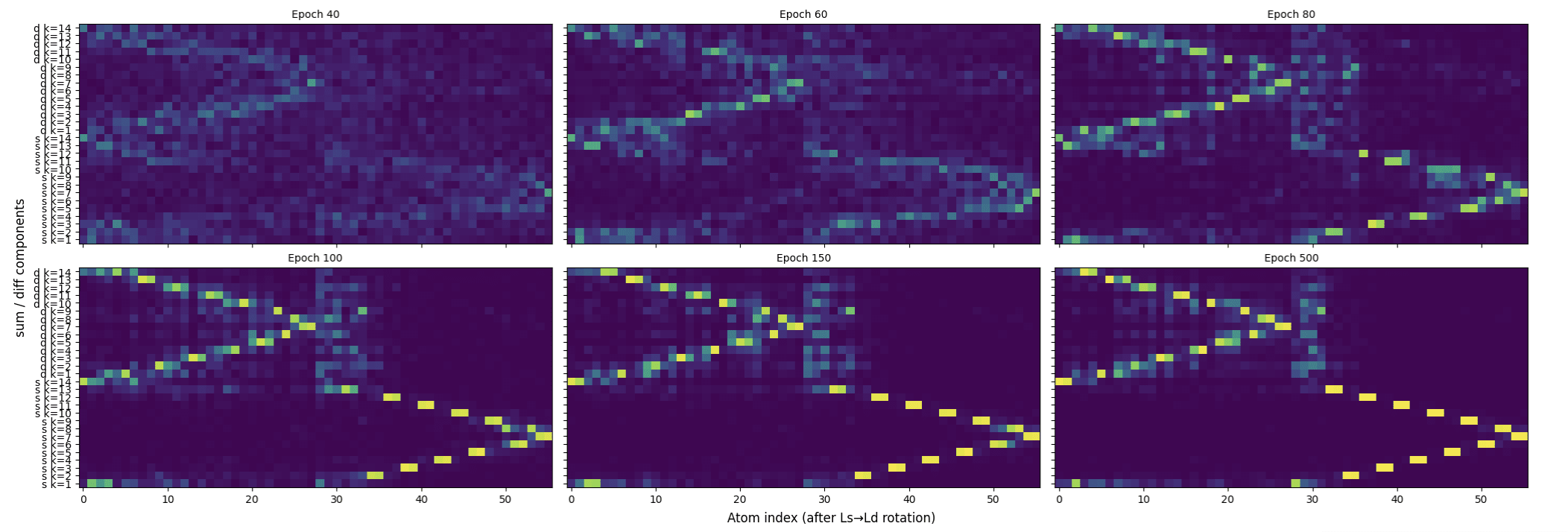
The paper also contains a similar figure showing alignment of the rotated eNTK eigenvectors in the first cliff with the '$a$' and '$b$' Fourier families, which is visible already at initialization.

Next steps

To summarize, we've found evidence that the eigenstructure of the empirical NTK aligns with learned features in well-known toy models for mechanistic interpretability. Hopefully, this is not just a fluke of these models, but is a promising (if preliminary) sign that the eNTK can provide the foundation for a new class of interpretability algorithms in realistic models.

To test this hope, it will be important to extend our pipeline to Transformers. Going forward, we'd like to repeat this analysis first for small Transformers, then (if all goes well) for increasingly large and realistic language models.^[9] I hope to report on this direction in the future. 

1. ^{^}

   In the very early days of mechanistic interpretability, researchers sometimes assumed that neural networks assigned features to the activations of individual neurons, but we now think that this isn’t generically true. The current paradigm (SAEs) involves interpreting linear combinations of within-layer neurons, but this too is essentially a guess. In this post, we explore the hypothesis that there are other potentially natural degrees of freedom to interpret besides linear combinations of within-layer neurons.

2. ^{^}

   See e.g. the examples on page 13 of Sharkey et al. (2025) ("Open Problems in Mechanistic Interpretability"). 

3. ^{^}

   Note that we’re not claiming that the theoretical result (1) with $K$ being the kernel at initialization - i.e., the formula that one derives in the lazy limit - is a good approximation to the function that a neural network learns beyond the lazy limit. By using Eq. (1) with (2) evaluated at the end of training, the empirical NTK hypothesis is making a different proposal. In particular, in regimes where the NTK at initialization differs from the NTK at the end of training, the empirical NTK hypothesis evades the lore that the theoretical NTK approximation can’t capture feature learning. 

4. ^{^}

   The eNTK evaluated over all points in a dataset has shape $(N,N,C,C)$ for $N$ the size of the dataset, and $C$ the number of output neurons (classes). To do an eigendecomposition, we have to reduce it to two dimensions. For the TMS analysis, we flatten the eNTK into a shape $(NC,NC)$ matrix by stacking the per-class blocks $K^{}ij$ for $i,j\in 1,...C$ row-major in $i$ and column-major in $j$.

5. ^{^}

   In the paper, we sweep over rescaling columns of the Jacobian by $I^{}$ before building the eNTK to adjust for the fact that Toy Models of Superposition used an importance-rescaled MSE loss, while the theoretical NTK formula is derived for conventional MSE loss. This plot shows the result for $\beta =0.3$, while the paper also shows results for other $\beta$'s.

6. ^{^}

   Specifically, we follow the experiment setup in Gromov (2023) ("Grokking modular arithmetic").

7. ^{^}

   Namely, let the "$\cos a$" Fourier feature family be the set of distinct functions $\cos \left(2\pi ka/p\right)$, for different $k$'s. There are $\lfloor \frac{p}{2}\rfloor$ independent such functions because trig identities relate modes with arguments $x$ and $2\pi -x$. On the other hand, each set of cosine features comes paired with a set of sine features (to absorb random phase factors that appear in the analytic solution of Gromov (2023)), for a total count of $2\lfloor \frac{p}{2}\rfloor$. So each cliff has the right counting to have two such families.

8. ^{^}

   In the paper, I explain why the first cliff is present at initialization using the closed-form formula of the eNTK for this model.

9. ^{^}

   As an early sign that the eNTK may track nontrivial structure in realistic language models, Malladi et al. (2022) found that kernel regression with the eNTK (computed at the pretrained checkpoint) tracks fine-tuning performance on a selection of language model tasks, suggesting that the eNTK may have found useful features (at least for subsequent fine-tuning, although they don’t claim that the eNTK is a good global approximation for the full model).