Published on October 13, 2025 11:40 AM GMT
This post assumes familiarity with basic geometry and an interest in the limits of formal systems. No advanced mathematics required, though some sections go deeper for those interested.
The Question
Here's a task:
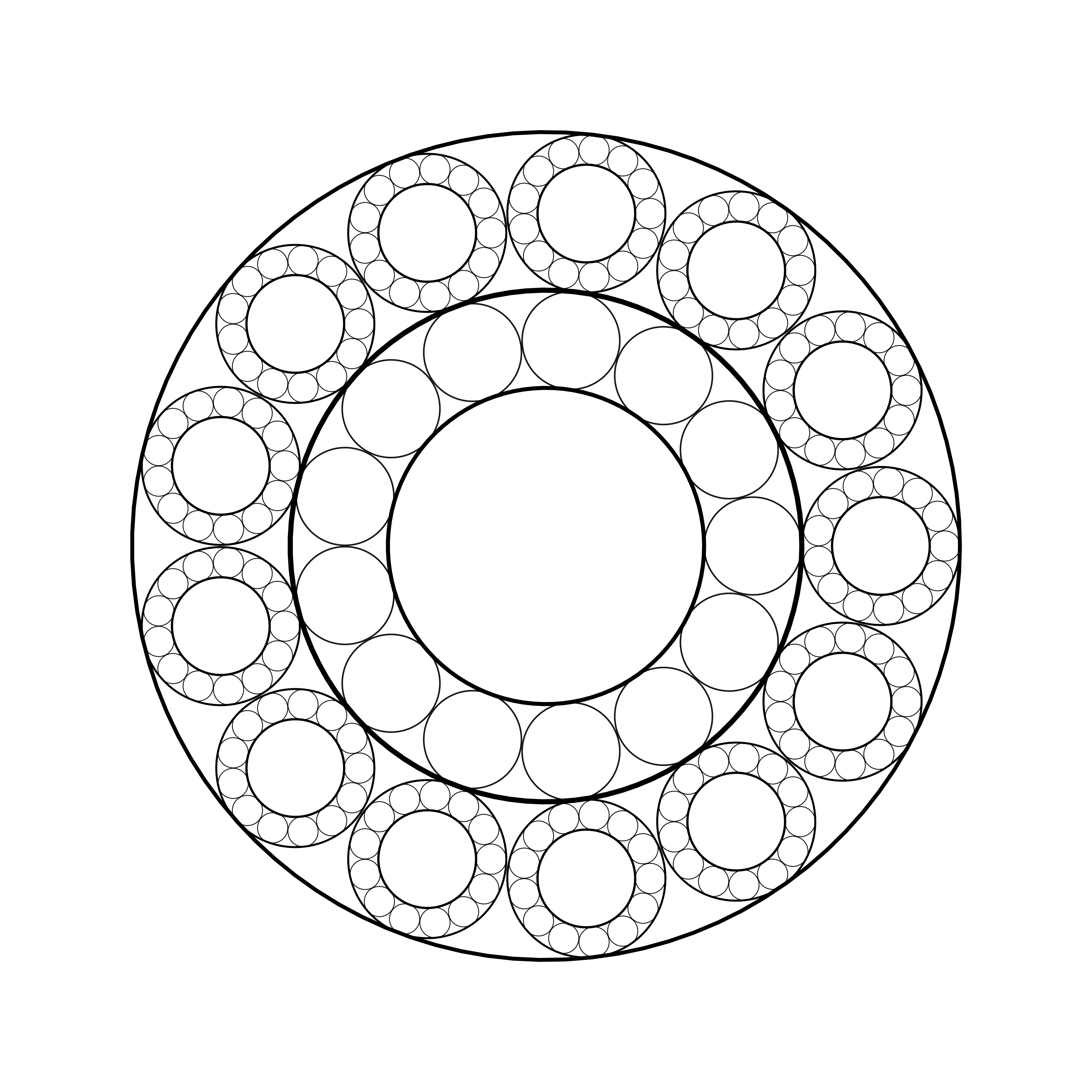
1. Draw a circle, rbig=1
2. Inside it, draw a smaller circle with radius rsmall=1/Φ≈0.618.
3. Between them, fit exactly 13 circles in a ring, of the size rring=(rbig−rsmall)2
4. Question: Do the 13 rings touch (are they tangential)?

Now, the easiest answer would be to calculate the 13-gon and to substract:
Outer radius:R=1Inner radius:rsmall=1Φ=Φ−1=√5−12Ring radius:rring=R−rsmall2=1−(Φ−1)2=2−Φ2=2−1+√522=3−√54Centers radius:rc=rsmall+rring=√5−12+3−√54=2(√5−1)+(3−√5)4=√5+14=Φ2Chord distance:d=2rcsin(π/13)=Φsin(π/13)Tangency requires:d?=2rringΦsin(π/13)?=3−√52sin(π/13)?=3−√52Φ=3−√51+√5=(3−√5)(1−√5)(1+√5)(1−√5)=3−3√5−√5+5−4=8−4√5−4=√5−2Numerical:sin(π/13)≈0.23932√5−2≈0.23607Difference:≈0.00325(numerical gap)
At first glance, our calculation seems to settle the question definitively. We've shown that for 13 golden ring circles to fit perfectly around a central circle—each one kissing its neighbors—we would need:
sin(π/13)=√5−2
And when we plug in the numbers, we get
0.23932≈0.23607.
They don't match, Case closed, right? Not quite.
Here's the subtle trap: those decimal approximations—0.23932 and 0.23607—are just that: approximations. We computed them to five decimal places, but what if they agree at the sixth? The millionth? We can never check infinitely many digits.
You might protest, we can compute more digits, and when we do, the gap persists. Yet this still doesn't constitute mathematical proof. We're comparing:
- sin(π/13): a transcendental number related to the 26th roots of unity√5−2∈Q(√5): an algebraic number from the golden ratio family
In the end, no finite computation can definitively prove these aren't equal.
The sophisticated response invokes field theory: sin(π/13) lives in a degree-6 extension of the rationals, while√5−2 lives in a degree-2 extension. Different degrees means they can't be equal.
This does prove inequality... but it's a "classical" existence proof. It tells us "they're definitely unequal" without giving us a constructive witness—no explicit polynomial we can exhibit, no certified lower bound on their difference.
The Obstruction
From a strict constructivist or finitist perspective, this abstract degree-counting doesn't provide the kind of tangible evidence we might want. It's like being told "there's definitely treasure buried somewhere in this field" but, it could be infinitesimal, or even negative treasure, and most importantly, the systems are too strong. √5,Φ are constructible via compass-and-straightedge, lives in finite field extensions,π,sin,eix requires analytic completion, limits, infinite processes. They all require completed infinities or non-constructive existence claims.

This particular geometric puzzle resists simple algebraic proof, and it traces back to one of the most beautiful impossibility results in mathematics: the discovery that polynomial equations of degree five or higher cannot, in general, be solved using radicals.
This is the Abel-Ruffini theorem, proved in the early 19th century, and it casts a long shadow over our circle-packing problem in ways that aren't immediately obvious.
When we ask whether sin(π/13) equals √5−2, we're not just comparing two numbers. We're asking whether a quantity that lives in the world of 13-fold symmetry—the realm of regular tridecagons and cyclotomic fields—can be expressed using the golden ratio, which lives in the much simpler world of √5.
The number sin(π/13) is algebraic. It satisfies a polynomial equation with integer coefficients. But here's the catch: that polynomial has degree six. And degree-six polynomials, being greater than or equal to five, fall on the wrong side of the Abel-Ruffini divide.
For polynomials of degree two, three, or four, we have formulas. The quadratic formula is taught in high school. Cubic and quartic formulas exist, though they're messy enough that most people never learn them. But for degree five and above? For most such equations, there simply is no formula involving only arithmetic operations and radicals. No amount of algebraic cleverness will extract an expression like√a+3√b+5√c that equals sin(π/13).
This isn't a limitation of human ingenuity. It's a fundamental structural fact about how polynomials and radicals relate to each other.
This creates an odd epistemic situation. We have three different ways of "knowing" that the circles don't quite touch:
First, we can compute. We can calculatesin(π/13) and √5−2 to a thousand decimal places, ten thousand, a million. The gap persists at every precision level we check. This is overwhelming evidence, but it's not proof—we can never check infinitely many digits.
Second, we can invoke Galois theory. The field-theoretic argument is airtight: these numbers live in extensions of the rationals of different degrees, so they cannot be equal. This is genuine proof, the kind mathematicians accept without reservation.
But third, we might want something more tangible: an logical polynomial we can exhibit, a certified lower bound on the difference, some algebraic witness to the inequality that doesn't require abstract machinery about field extensions. And this—precisely this—is what the n≥5 obstruction denies us.
This is what makes the golden circle packing with 13 rings philosophically interesting. It sits in a peculiar limbo: perfectly well-defined geometrically, numerically computable to arbitrary precision, provably non-tangent by abstract algebra, yet algebraically unwitnessable due to a fundamental obstruction that emerges exactly at degree five.
Discuss

