Published on October 10, 2025 10:50 PM GMT
I Context
Michael Nielsen and Davidchapman had an interesting conversation on twitter recently about understanding things deeply. David expanded on what he meant in the last tweet. It's interesting reading.
All of that is to say, what it means to understand something deeply? I've had scattered thoughts on this topic over the past few years, and decided to write down how my understanding of what it feels like to understand has evolved. The following is a stylized account.
II Evolution
Years ago, I sat through a classical mechanics exam in my first year at university, whilst a migraine clouded my thoughts. I remember desperately flitting between ideas that no longer made sense, machinery I had forgotten how to operate, and intuitions which could not be bound to formalism. As I fell down an abstraction stack I could no longer navigate, I failed to grab hold of any knowledge that could form a firm ground for me to stand upon and build back up towards celestial mechanics. Needless to say, I failed.
But that experience stuck with me as an example of what it's like to no longer understand something. A bit extreme perhaps, but it's helped improve my sense of when I don't understand a topic. Infallible, of course, and it requires me to pay attention to the sensation. But now I know what the sensation is.
Or, at least, I thought I did.
Years later, at my local rat meetup, we were working through problems in thinking physics. We were stuck on one, how will an empty cube move if you remove one side in the presence of air? It felt like I knew what the answer should be, but when I tried grabbing the intuition from the murky depths and pulling it into view of my mind's eye, it kept slipping away. Something to do with how empty tankers collapse if you poke a hole in them. The meetup ended, but I still had no answer. Bull-minded as I was that day, I kept thinking about it for a few hours.
Then it hit me: take a hand-pump, pull till it creates a vacuum, and it snaps forward and jerks to a halt. Suddenly, I could feel how the cube would have to move. There was a sense of physical necessity to it. I wasn't dealing with a bit of formal argumentation any more. Instead, I was remembering events in my life and calling up the parts of myself that knew reality could only move one way from there, and giving words to that causal structure.
And then I understood that for my entire life, I'd almost never really understood a piece of physics. The firm ground I believe I stood on was no more than sand.
I'd love to say that this insight shocked me into a state of urgency and I rushed about seeking firm ground from which to rebuild my understanding of the world. I didn't. But what did happen is that my sense of what it is like to understand what refined, now that I had a gold standard to which to compare other things to. And I updated all the way that if I underestimated how deeply I can understand something at a gut level, I'm probably still unaware of the heights of understanding. No doubt, when Feynman says he does not really understand something, he's placing the bar a few rungs above where my scale stops.
Except there were more surprises in store for me. In spite of my mental library now holding one example of deep understanding, it was only one example. Hardly enough to generalize from. You can't even interpolate with only one data-point! And I don't do well out of distribution. Physical knowledge was the distribution and mathematics was outside it.
I realized this a few weeks later when I understood a new proof deeply. Namely, the obvious proof of why injective maps have a left inverse trivially but surjective maps having a right inverse requires the axiom of choice. At first, I just proved the claim, which was obvious enough. But I didn't have a mental image. I didn't have the sense that reality had to be this way. And recalling my sense that more was possible, I tried to understand the proof more deeply.
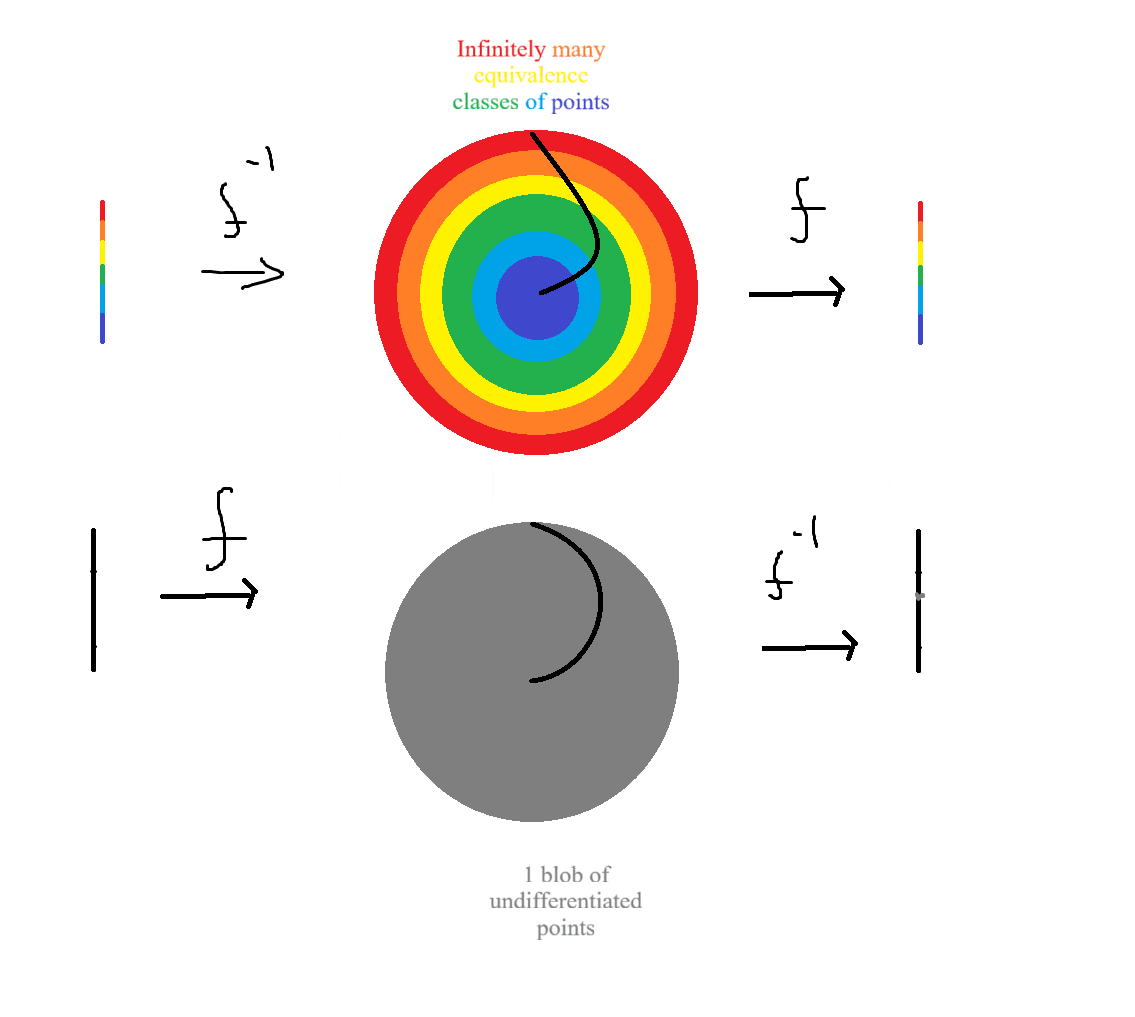
Eventually, I stumbled onto a mental movie, one literally highlighting the core concepts in the proof. Suddenly, the conclusion felt necessary and not just obvious.
What do I mean by "just obvious"? Sometimes, when reasoning your mind might jump to a conclusion. Surely it's happened before? "Oh, f′′(x)=−kx, that's clearly an oscillator." You know what the answer has to be. Perhaps it's a bit less crisp than that, like when you realize you have a problem with your breaks when you can't halt your car quickly enough.
But the realization is just a proposition, a belief. You don't feel the huge causal model you have of reality forcing you to this particular conclusion. It's just intuition, not post-rigorous-intuition you can cash out into a great tower of reasoning scaffolded about sturdy pillars and built upon a rock solid foundation. Instead, it's just dirt floating in the void.
What felt curious about this insight is that I would not have been able to predict the particular texture of deeper understanding in mathematics. It doesn't feel the same as in physics.
As an analogy, imagine you encounter the color red for the first time. Over time, you see brighter and brighter hues, which you couldn't have conceived of before. Then, you see blue for the first time. Immediately, you know that there should be other hues, but you can't really imagine what they'd look like.
Which led me to the realization the feeling of deep understanding varies field by field. So someone who has cultivated a very fine sense for understanding in, say, mathematics, who can tell in an instant when they do not understand something because they've been in this situation before, need not have anywhere near as refined a sense for understanding in other areas. That is, a great mathematician can engage in shoddy reasoning about society without realizing it is shoddy. Likewise for other great minds.
Fine. If one is not enough, then two. If not two, then three. If not three, then more. Just because it is hard to generalize from one sensation, doesn't mean you can't generalize from more examples. Three good examples is a lot, enough to learn the latent structure of many different structures. Perhaps even the structure of understanding itself.
III Pedantry and Questions
OK, ok, so I might have simplified things somewhat. Like, the distinction between something that you find obvious and something that you deeply understand isn't a binary. It's more of a spectrum. Likewise, it's not the case that you only have firm ground to stand on or are in free-fall. All valid points, and also all pedantry. (Of course, one wants to be a pedant in many cases...)
But I think the simplified model was good enough to get my point across. It should be fairly obvious that between rock solid ground you can bet your life on and a free-fall into insanity, you can have some muddy ground that you can't build the pyramids on, but it'll do for a walk in your wellies. Like, I don't know, taking astronomers on trust when they say the moon is 384,000 km away. Can you feel the necessity of it? I can't. But I understand that figure enough to calculate the velocity of the moon.
OK, that's the pedantry out of the way. Onto some questions I have. What are the higher levels of understanding like? I'm sure they exist, but I don't recall experiencing them. Is there a single hierarchy, or is it more like a tree? How well can you generalize your feelings of understanding? If, say, you have a refined sense of what it means to understand classical mechanics, does that sense generalize to quantum mechanics? Do these senses require something like a geometric or kinaesthetic sense, or can they be more abstract? Can you interpolate between the sensations like you can interpolate with enough examples of colour?
I don't know. But I'm keen to find out.
Discuss

