🔢 **数学的严谨性挑战：** 文章指出，直观地认为无穷级数 1+1/2+1/4+1/8+... 等于 2，以及对无限项等式的运算（如加法、乘法）存在定义上的空白和潜在的逻辑问题。这表明在数学中，直觉需要严谨的定义和证明来支撑，尤其是在处理无限概念时。

🔢 **序列与收敛的定义：** 为了严谨地处理无限问题，文章引入了“序列”（sequence）的概念，即一个有序的无限数字列表。在此基础上，文章详细阐述了序列“收敛”（convergence）的数学定义，从“越来越接近”的模糊表述，逐步精炼到“对于任意小的正数 ε，都存在一个临界点 k，使得序列从第 k 项开始，所有项与极限值 A 的差的绝对值都小于 ε”的精确定义。

সংখ **序列加法的性质与记法：** 文章通过证明，说明了当两个收敛序列相加时，它们的和序列也收敛，且其极限是原序列极限的和。同时，文章解释了数学家为何有时会省略“极限”的符号，直接写出无限求和等于某个值（如 ∑∞k=0(1/2)^k = 2），这不仅是图省事，更暗示了在特定条件下，无限求和可以被视为一种“合法的”操作，为数学发现提供了线索。

Published on October 8, 2025 7:44 PM GMT

This is a prototype attempt to create lessons aimed at teaching mathematical thinking to interested teenagers. The aim is to show them the nuts and bolts of how mathematics is built, rather than to teach them specific facts or how to solve specific problems. If  successful I might write more.

Calculate $1+\frac{1}{2}+\frac{1}{4}$+116+⋯

What you'll quickly notice (or might already be aware of) as you keep on adding smaller and smaller steps is that it gets closer and closer to 2 but never quite gets there.

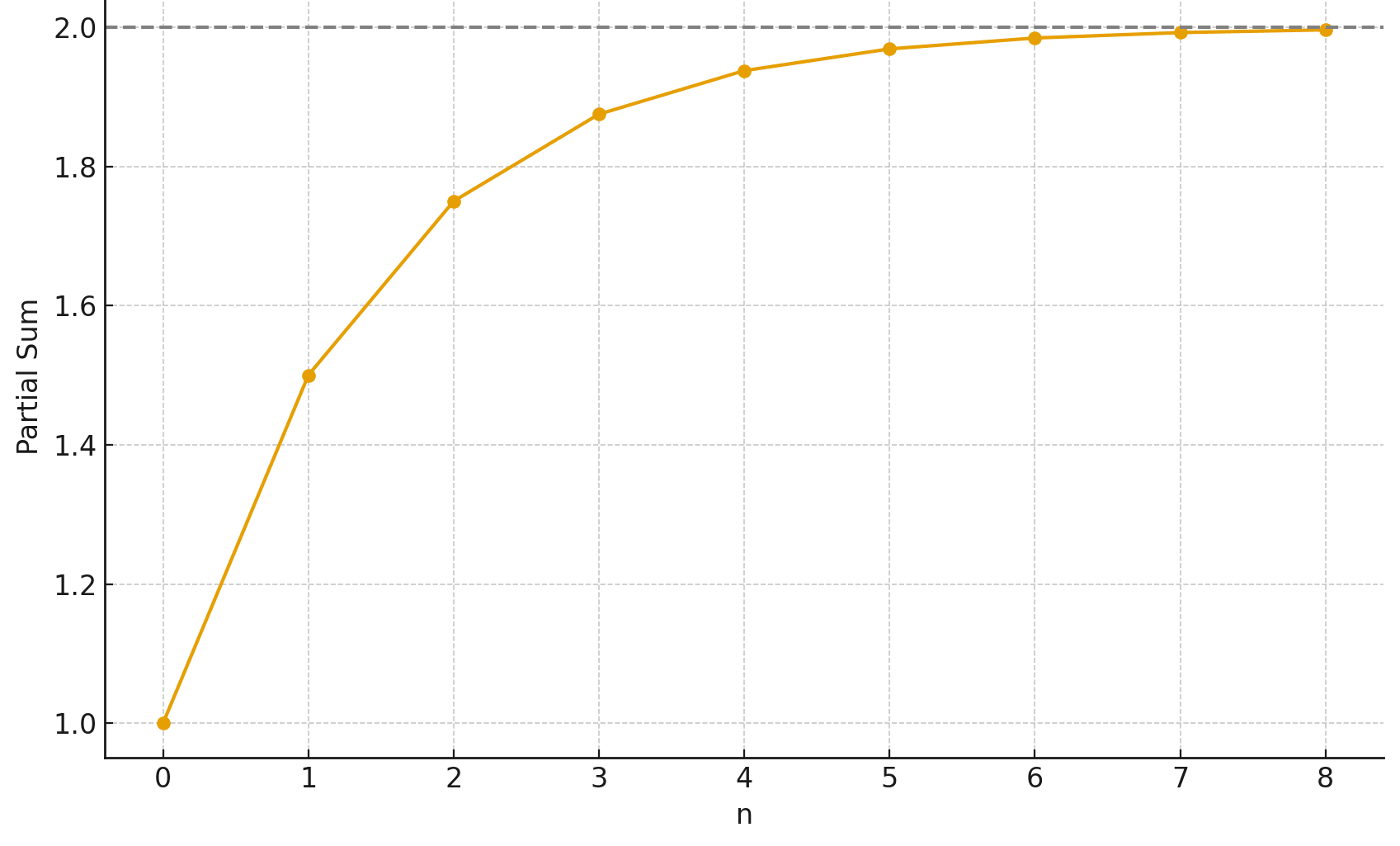
Now you might be tempted to say that $1+\frac{1}{2}+\frac{1}{4}$+116+⋯=2

When we see an equation like a = b, that implies certain things:

E.g. $a+1=b+1$

E.g. If $c=d$, then $a\bullet c=b\bullet d$.

We've defined what it means for an equation to have a finite number of terms on one of the sides. We've never defined what it means for an equation to have an infinite number of terms. Do all those rules we have about equations apply to these infinite term equations too? 

If $1+\frac{1}{2}+\frac{1}{4}$+116+⋯=2 and $\frac{1}{2}+\frac{1}{4}$+116+132+⋯=1, does 1 + $\frac{1}{2}+\frac{3}{4}$+316+332+⋯=3?

What about if we multiply the two together? Does $(1+\frac{1}{2}+\frac{1}{4}$+116+⋯)∙(12+14+18+116+132+⋯)=2∙1=2?

What does it even mean to multiply two infinite sums together?

To answer all these questions we need to define everything in terms of things we already understand. Then we can try and prove properties about them.

The first step is to break our infinite terms into something that only has finite terms. To do that we stop talking about vague things like infinite sums, and start talking about sequences.

A sequence is just a neverending list of numbers. 1,2,3,4... is a sequence, as is 1,4,9,16...

More formally it's a mapping from the positive integers to the reals^[1]. If you tell me you have a sequence $s$, I need to be able to ask you what the 172nd element of $s$ is, and you need to be able to answer me. We denote this as $s_{172}$.

In our case, we can define a sequence:

$sum{s}_n={\sum }^{}$

In other words, for any integer $n$, the $n$th number in the sequence $sums$ is the sum of the first $n$ terms in  $1+\frac{1}{2}+\frac{1}{4}$+116+⋯=2. Now because we're only ever dealing with a finite number of terms, every member of this sequence is well defined.

Now we want to define a property called convergence, and say that $sums$ converges to 2. How might we define that?

Our first attempt might be to say that:

A sequence $s$ converges to $A$ if for all $n$, $s_n$ is always closer to $A$ than $s_{n-1}$.

But a bit of exploration proves that is totally insufficient - By that definition $sums$ converges to 3, 17, and in fact any number greater than 2.

So let's try and address that in our next attempt:

A sequence $s$ converges to $A$ if for all $n$, $s_n$ is always closer to $A$ than $s_{n-1}$, and $s_n$ eventually gets infinitely close to $A$.

But we can't just willy nilly throw around terms like infinitely close. We need to define convergence only in terms of things we already understand. What we want to express is that if you pick any value, the sequence eventually gets closer to A than that value. We can express that precisely as:

A sequence $s$ converges to $A$ if for all $n$, $s_n$ is always closer to $A$ than $s_{n-1}$, and for any non-zero number $ϵ$, there is a number $k$, such that $|A-s_k|<ϵ$^[2].

That works for all the examples we've given so far. But it doesn't work for some other examples. What about:

$sine{s}_n=\frac{\sin \left(n\right)}{n}$

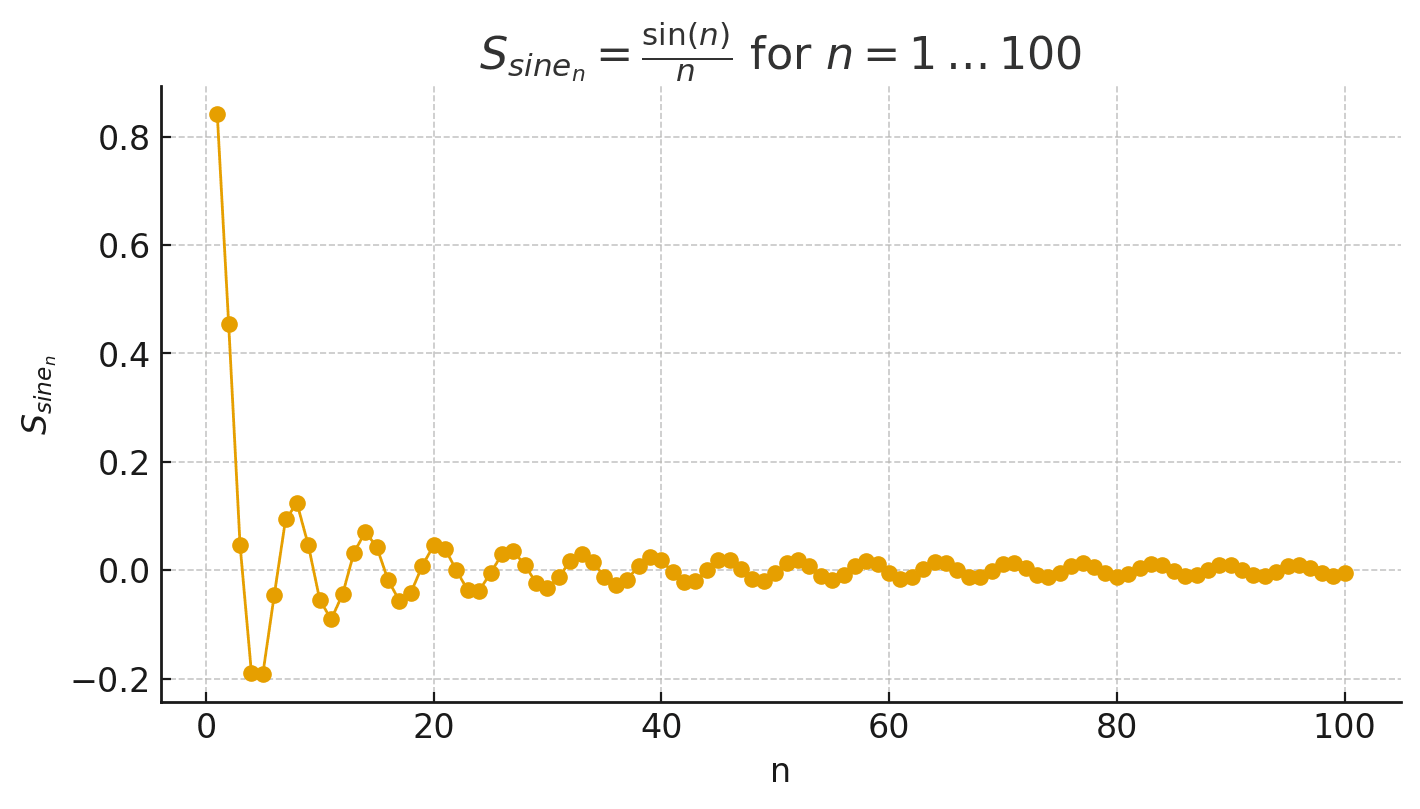
We definitely want to be able to express somehow that the value of this sequence is 0, but it doesn't fit our definition, since it doesn't continuously get closer to 0 it keeps on overshooting, but the amount it overshoots by keeps getting smaller.

So we need to loosen our criteria. Instead of requiring it to always get closer to A, we can say that for any number, the sequence needs to eventually get closer to A than that number, and stay there:

A sequence $s$ converges to $A$ if for any non-zero number $ϵ$, there is an integer $k$, such that for all integers $m$, where $m>=k$,  $|A-s_m|<ϵ$.

And this is indeed the most common definition of convergence that mathematicians use.

With this tool we can now start to explore concrete questions about convergence.

For example lets define the sum of two series as follows:

$s3=s1+s2$ if $s{3}_n=s{1}_n+s{2}_n$.

Now if $s1$ converges to $A$, and $s2$ converges to $B$, does $s3$ necessarily converge to $A+B$?

We can attempt to sketch out a proof:

For any nonzero number $ϵ$, there is a value $k_1$ such that for all $m\ge k_1$, $|s{1}_m-A|<\frac{ϵ}{2}$ and a value $k_2$ such that for all $m\ge k_2$, $|s{2}_m-B|<\frac{ϵ}{2}$. Without loss of generality^[3], assume that $k_1\ge k_2$. Then for all $m\ge k_1$, we have $|(s{1}_m+s{2}_m)-(A+B)|\le |s{1}_m-A|+|s{2}_m-B|<\frac{ϵ}{2}+\frac{ϵ}{2}$.

Not only does this prove that adding sequences works as we expect, it also hints that when we do so the resultant sequence converges nearly as fast as the slowest of the two constituent sequences. Convergence speeds are a relatively advanced topic, but you can bet that the first thing you'll do if you study it is try to define precisely what it means for a sequence to converge quickly or slowly.

Now the usual notation for $s$ converges to $A$ is:

${lim}_{n\to \infty }{s}_n=A$

However you'll sometimes see mathematicians skipping this notation. Instead of writing ${lim}_{n\to \infty }{\sum }^{}$=2 they'll just write: ${\sum }^{}$=2.

What's going on here?

Firstly Mathematicians are lazy, and since everyone who reads the second form will understand it means the same thing as the first, why bother writing it out in full?

But it's actually hinting at something deeper - when you work with limits of sums they often behave as though you literally are just adding an infinite number of terms. Manipulations like the one Euler used for the Basel problem often happen to work even though they aren't actually justified by our definitions, and this notation can give you the hint you need to attempt just such an "illegal" manipulation before you commit yourself to finding a full blown formal proof.

Later mathematicians then discovered some of the conditions under which you can treat a limit as a normal sum, and so such loose notation can actually provide fertile ground for future mathematical discoveries. This isn't an isolated event - such formalisation of informal notation has been repeated across many disparate branches of mathematics.

1. ^{^}

   It doesn't have to be the reals - you could have a sequence of functions or shapes or whatever, but for our purposes it's the reals.

2. ^{^}

   Those vertical lines mean the absolute value, which means to ignore whether the value is positive or negative. So $|-3.4|=\left|3.4\right|=3.4$. Here it's just used to express that $S_k$ and $A$ are less than $ϵ$ distance apart, without specifying whether $S_k$ is greater than or less than $A$.

3. ^{^}

   Without loss of generality is another way of saying that we're going to prove one scenario (here where $k1\ge k2$), but the proof is identical in other scenarios (e.g. when $k2>k1$) if you just switch the symbols around (so call $S1$ $S2$ and vice versa), so we don't want to repeat the proof multiple times for each scenario.