The T-maze, shown below, is a prototypical example of a task studied in the field of reinforcement learning. An artificial agent enters the maze from the left and immediately receives one of two possible observations: red or green. Red means that the agent will be rewarded for moving to the top at the right end of the corridor (in the question mark tile), while green means the opposite: the agent will be rewarded for moving down. While this seems like a trivial task, modern machine learning algorithms (such as Q-learning) fail at learning the desired behavior. This is because these algorithms are designed to solve Markov Decision Processes (MDPs). In an MDP, optimal agents are reactive: the optimal action depends only on the current observation. However, in the T-maze, the blue question mark tile does not give enough information: the optimal action (going up or down) depends also on the first observation (red or green). Such an environment is called a Partially Observable Markov Decision Process (POMDP).
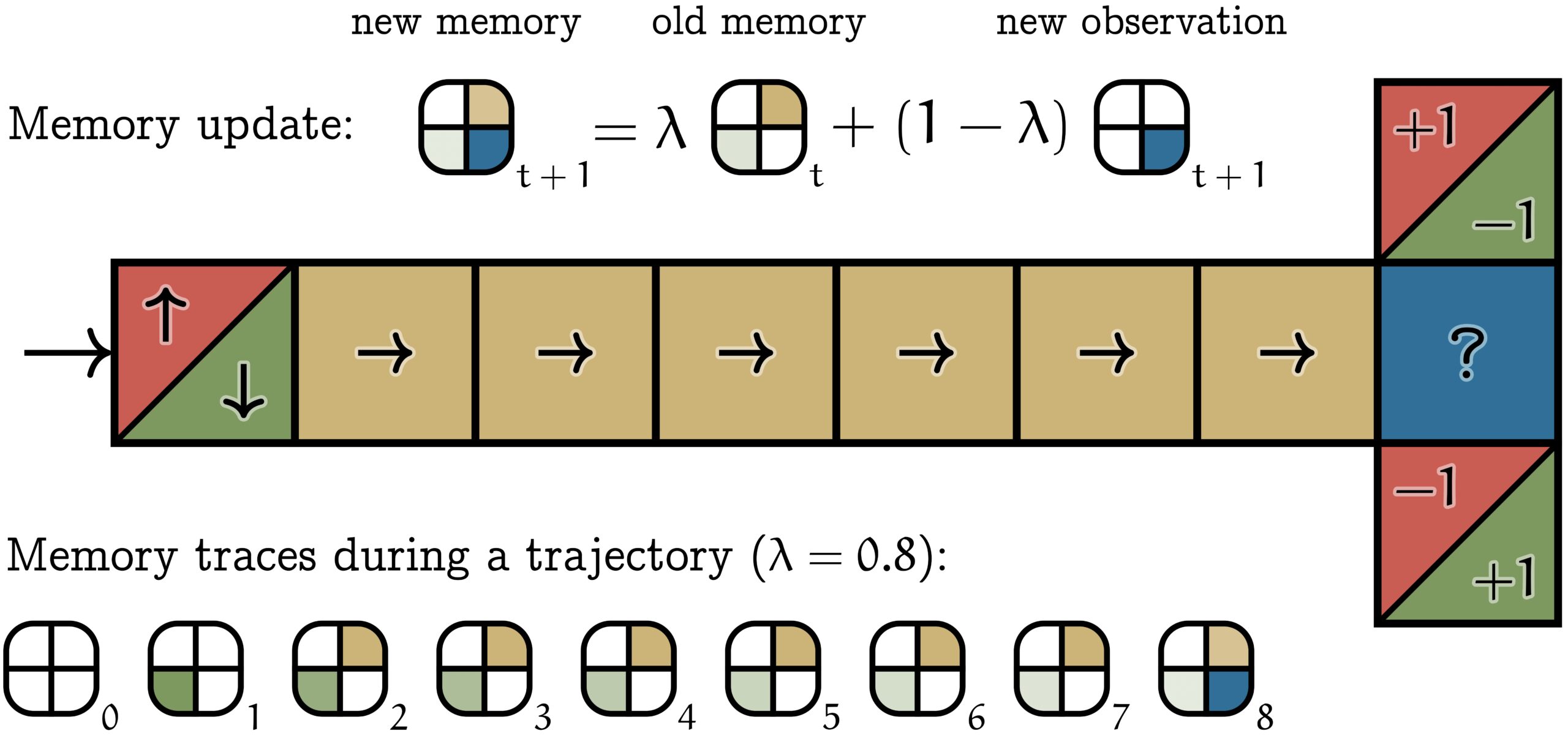
In a POMDP, it is necessary for an agent to keep a memory of past observations. The most common type of memory is a sliding window of a fixed length . If the complete history of observations up to time is 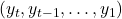 , then the sliding window memory is
, then the sliding window memory is  . In the T-maze, since we have to remember the first observation until we reach the blue tile, the length of the window has to be at least equal to the corridor length. The problem with this approach is that learning with long windows is expensive! We can show [1] that learning with windows of length generally requires a number of samples that scales exponentially in . Thus, learning in the T-maze with the naive sliding window memory is not tractable if the corridor is very long.
. In the T-maze, since we have to remember the first observation until we reach the blue tile, the length of the window has to be at least equal to the corridor length. The problem with this approach is that learning with long windows is expensive! We can show [1] that learning with windows of length generally requires a number of samples that scales exponentially in . Thus, learning in the T-maze with the naive sliding window memory is not tractable if the corridor is very long.
Our new work introduces an alternative memory framework: memory traces. The memory trace is an exponential moving average of the history of observations. Formally, 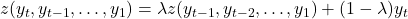 . The forgetting factor
. The forgetting factor 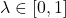 controls how quickly the past is forgotten. This memory is illustrated in the T-maze above. There are 4 possible observations (colors), and thus memory traces take the form of 4-vectors. In this example, the initial observation is green. As the agent walks along the corridor, this initial observation slowly fades in the memory trace. Once the agent reaches the blue decision state, the information from the first observation is still accessible in the memory trace, making optimal behavior possible.
controls how quickly the past is forgotten. This memory is illustrated in the T-maze above. There are 4 possible observations (colors), and thus memory traces take the form of 4-vectors. In this example, the initial observation is green. As the agent walks along the corridor, this initial observation slowly fades in the memory trace. Once the agent reaches the blue decision state, the information from the first observation is still accessible in the memory trace, making optimal behavior possible.
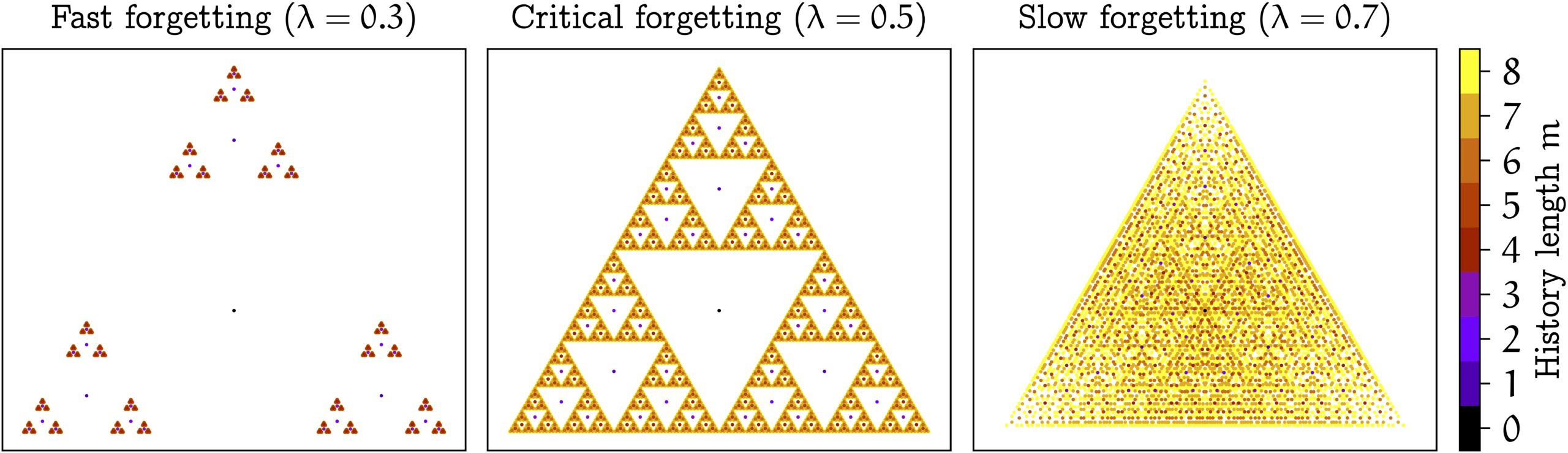
To understand whether memory traces provide any benefit over sliding windows, it is helpful to visualize the space of memory traces. Consider the case where there are three possible observations: 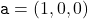 ,
, 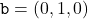 , and
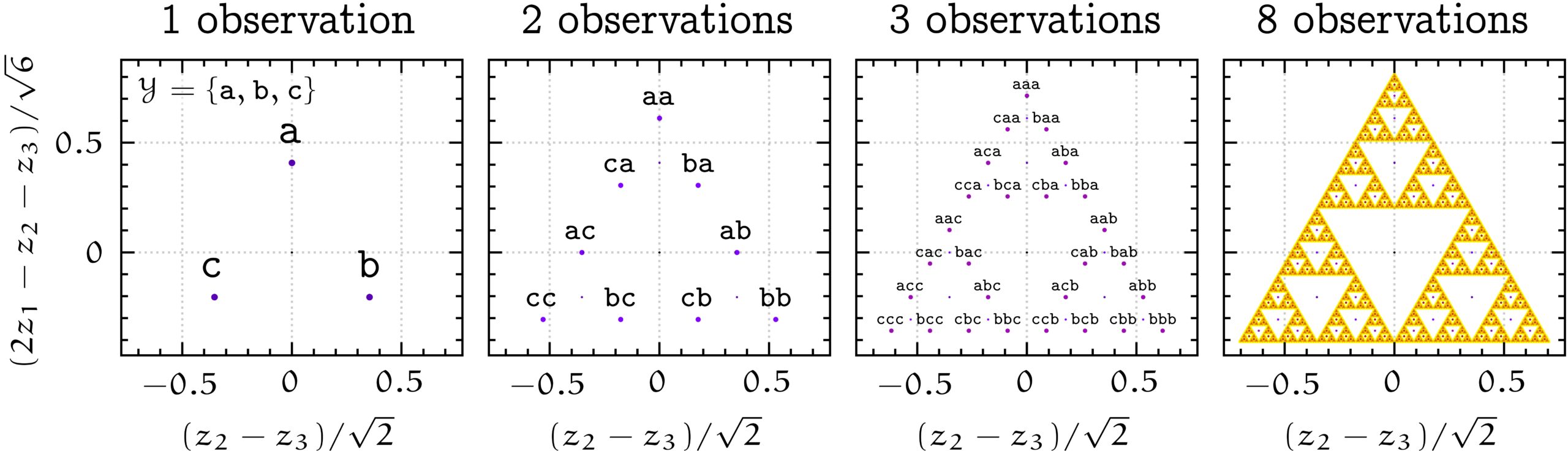
, and 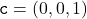 . Memory traces are linear combinations of these three vectors, but in this case it turns out that they all lie in a 2-dimensional subspace, so that we can easily visualize them. The picture below shows the set of all possible memory traces for different history lengths with the forgetting factor
. Memory traces are linear combinations of these three vectors, but in this case it turns out that they all lie in a 2-dimensional subspace, so that we can easily visualize them. The picture below shows the set of all possible memory traces for different history lengths with the forgetting factor 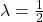 . The set of memory traces forms a recursive Sierpiński triangle.
. The set of memory traces forms a recursive Sierpiński triangle.
The picture changes if we vary the forgetting factor , as shown below.

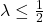 , then memory traces preserve all information of the complete history of observations! In this case, we could theoretically decode all previous observations from a single memory trace vector. The reason for this property is that we can identify what happened the past by zooming in on the space of memory traces.
, then memory traces preserve all information of the complete history of observations! In this case, we could theoretically decode all previous observations from a single memory trace vector. The reason for this property is that we can identify what happened the past by zooming in on the space of memory traces.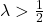 (“slow forgetting”) can significantly outperform sliding windows in certain environments. In fact, the T-maze is such an environment. While the cost of learning with sliding windows scales exponentially with the corridor length, for memory traces this scaling is only polynomial!
(“slow forgetting”) can significantly outperform sliding windows in certain environments. In fact, the T-maze is such an environment. While the cost of learning with sliding windows scales exponentially with the corridor length, for memory traces this scaling is only polynomial!