文章深入探讨了里德堡原子阵列在量子计算和量子模拟领域的快速发展。自概念提出以来，量子计算经历了多种物理系统的探索，目前超导电路和离子阱占据主导，但里德堡原子阵列作为一种新型候选系统，正展现出巨大潜力。文章详细介绍了里德堡原子的特性、基于其的量子信息处理原理，以及通过冷原子显微镜和大规模原子阵列技术实现的突破。特别是，Lukin和Greiner教授团队在构建无缺陷原子阵列方面的进展，为量子模拟器和通用量子计算奠定了基础。该技术已成功应用于解决复杂优化问题，并催生了QuEra Computing和Pasqal等初创公司，预示着其在未来量子技术领域的重要地位。

⚛️ **里德堡原子阵列的独特优势**：里德堡原子（n=50-100的高激发态）具有长寿命和较大的偶极矩，使其能够实现远距离的直接耦合，并利用偶极阻塞效应实现量子比特的定义和通用量子逻辑门的构建。这为构建大规模、可编程的量子模拟器和通用量子计算机提供了独特的物理基础。

🔬 **关键实验技术的突破**：实现大规模里德堡原子阵列的关键在于精确控制每个光阱中的原子数量。通过冷原子显微镜技术，研究人员能够探测和控制单个原子，克服了实验上的巨大挑战。Lukin和Greiner教授团队在2016年实现了包含100个光镊阵列的大规模无缺陷里德堡原子阵列，为后续研究奠定了坚实基础。

💡 **技术发展与应用前景**：自2016年以来，里德堡原子阵列技术发展迅速，已成功模拟复杂的量子多体模型，并应用于解决NP-hard优化问题（如最大独立集合问题），展现出潜在的量子加速优势。Lukin和Greiner教授团队通过QuEra Computing公司，以及Browaeys教授的Pasqal公司，正在积极推动该技术的产业化，预示着其在未来量子计算和模拟领域的光明前景。

🌍 **全球合作与人才汇聚**：里德堡原子阵列技术的发展得益于国际顶尖研究团队的合作，包括来自俄罗斯、德国和法国的科学家。美国哈佛大学通过汇聚Lukin和Greiner等人才，在该领域占据了领导地位。同时，中国科学家也积极参与其中，展现了该技术吸引全球顶尖人才的趋势，预示着其未来持续的进步和创新。

量子计算与量子模拟概念提出到今天有40多年了，基于离子阱的量子计算出现到今天也有27年了。过去这二三十年，是量子计算与量子模拟技术大发展的时代，为了寻找最合适量子计算的量子比特，人们找遍了各种物理系统：离子阱、单光子、冷原子、量子点、超导电路、金刚石色心……最近几年，量子计算的实用化曙光初现，量子计算研发的投入已经越来越多的集中到超导电路和离子阱两个物理系统中，实用的量子计算机似乎就要在这两个系统中一决雌雄了。但其它物理系统也并没有止步不前：里德堡原子系统、硅基量子点系统和光子系统都取得了长足进步。我一直对新型量子计算候选系统保持着兴趣，并持续做了一些文献追踪。在这里，我简单介绍一下光悬浮里德堡原子阵列量子模拟与计算的发展进程。

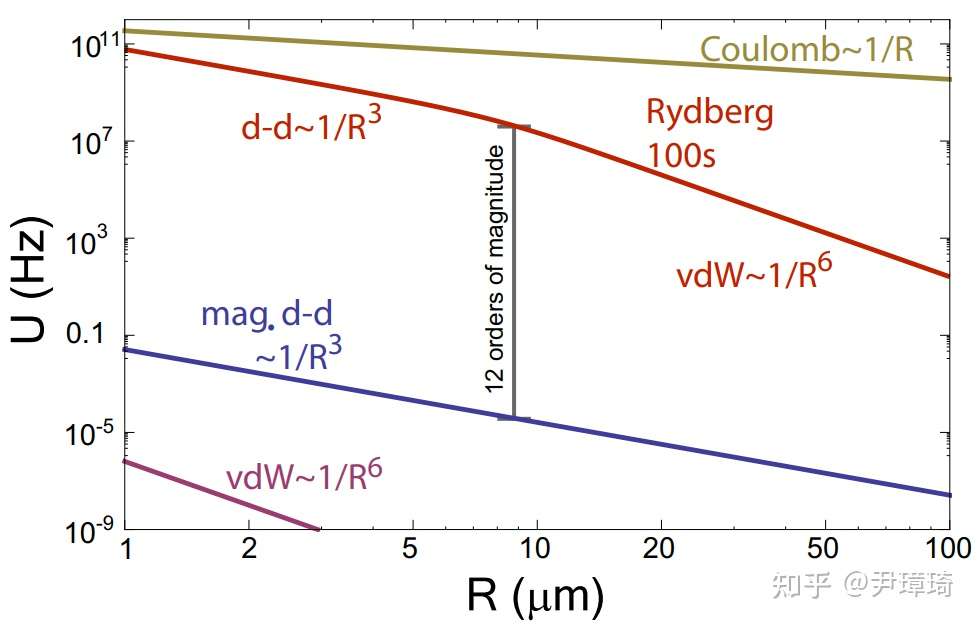
里德堡原子通常是指被激发到轨道数n=50-100的高激发态原子，此时能级的寿命达10微秒量级，原子轨道半径在微米量级。里德堡原子具有很大的偶极矩，可以实现相聚遥远的里德堡原子之间的直接耦合，如图一所示。基于里德堡原子的量子信息处理，最早是2001年由M. Lukin等人所提出的：他们提出把一团里德堡原子囚禁在光阱中，由于里德堡原子之间的偶极阻塞效应，导致里德堡原子团的集体激发能级并不是等间距的。我们可以实现单激发状态，从而定义量子比特以及通用量子逻辑门。基于此技术路线，人们可以实现里德堡原子团与单光子之间的相干耦合，基于里德堡原子团的量子网络等。2010年，在 Rev. Mod. Phys. 上有一篇关于里德堡原子信息处理的综述。

要让里德堡原子发挥全部潜力，需要实现大规模的原子阵列，在每个光阱中确定性地囚禁一个原子，通过激光激发原子到里德堡态，从而实现近邻里德堡原子间的量子逻辑门，以及基于里德堡原子阵列的量子模拟。2002年，德国马普所Bloch组的M. Greiner等人在光晶格中装载了温度在nK量级的超冷Rb原子，通过激光调控原子的相互作用，实现了从超流体到Mott绝缘态的相变。虽然原子冷却到nK温度后，可以被稳定高效囚禁在光晶格中，但是如何让每个晶格只囚禁一个原子，一直是实验上的巨大挑战。2005年，M. Greiner去美国哈佛大学建立自己的研究组。2009年，他发明了冷原子显微镜，可以探测到光晶格中的单个原子。他们用此技术实现了单原子精度超流体到Mott绝缘体转变过程的测量，量子多体系统的纠缠熵，以及多体局域系统的量子纠缠等。冷原子显微镜技术为里德堡原子阵列量子模拟器扫平了障碍。

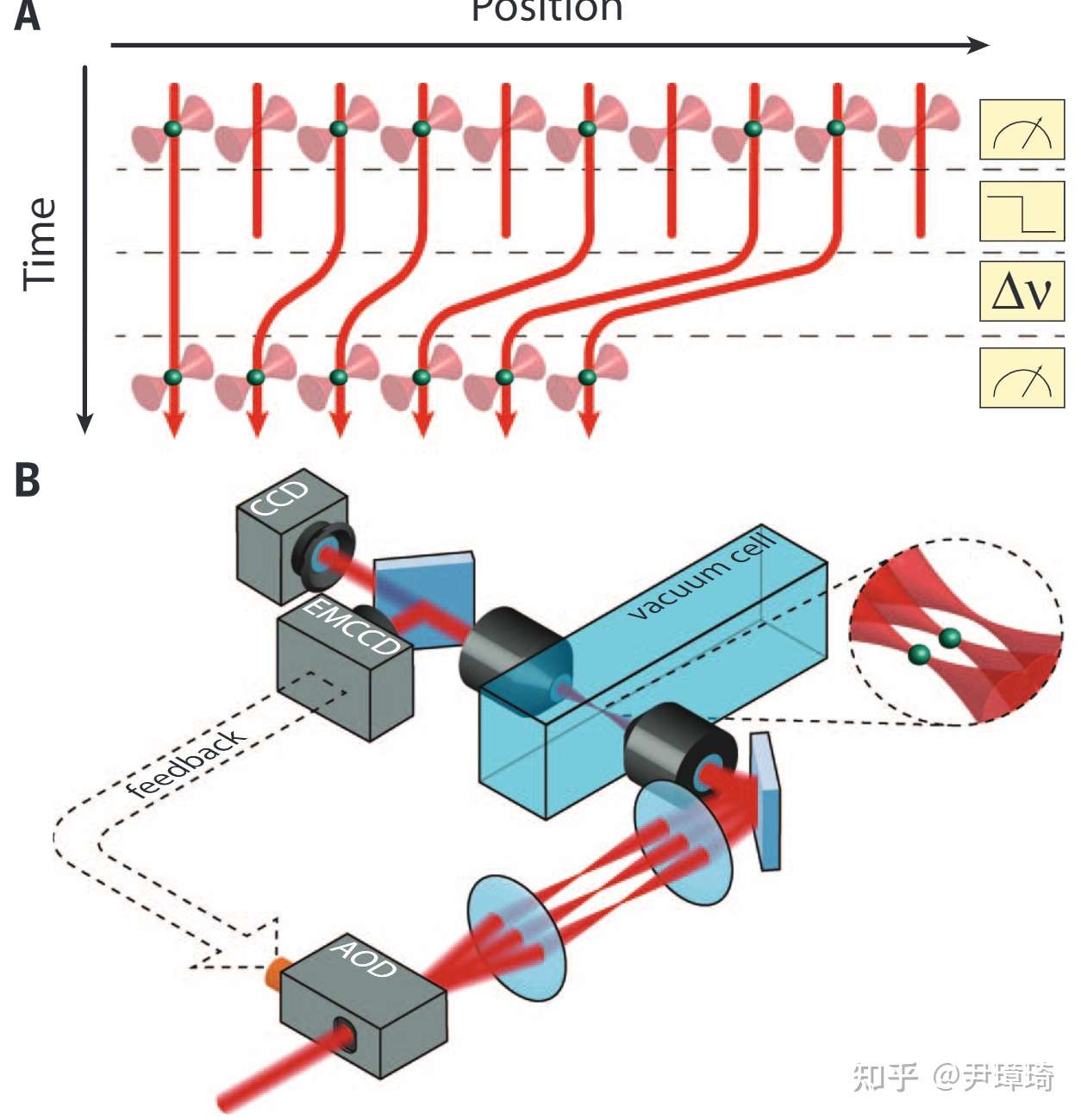
2016年，Lukin教授与Greiner教授合作，完成了大规格里德堡原子阵列的实验。他们先实现100个光镊阵列，并把激光冷却的原子团加载在这个光镊阵列上。。然后给这个光镊阵列拍照，识别出每个光镊中到底有没有原子。通过对荧光计数进行统计分析，还可以确认每个光镊中最多只有一个原子。然后调控那些占据了原子的光镊位置，可在1秒内实现包含大于50个里德堡原子的无缺陷光镊阵列，如图二所示。法国国家科学研究中心的Antoine Browaeys教授组也独立实现了无缺陷的2维里德堡原子阵列。

此技术发明后，里德堡原子阵列量子计算与量子模拟步入了快车道。2017年Lukin组实现了51个里德堡原子阵列Ising型量子多体自旋模型，并研究其多体动力学。通过激光可操控原子的内态，从而打开和关闭原子之间的耦合，并对系统的相互左右哈密顿量进行编程调控。2021年，Lukin组和Browaeys组各自独立的实现了包含数百个里德堡原子阵列的量子模拟器：Lukin组实现了包含256个里德堡原子的多体自旋模型以及反铁磁相变，Browaeys组实现了196个里德堡原子的二维反铁磁相，实验数据与数值模拟之间匹配得很好。接下来，Lukin组又实现了里德堡原子的高速高保真度传输与可控的量子逻辑门，并制备了多体纠缠的图态、表面码量子纠缠态等。这昭示了此系统不仅能作为可编程的量子模拟器，还具备通用量子计算的潜力。

随着技术的迅速进步，里德堡原子阵列已经在很多问题上找到了应用。2022年初，Lukin组发表论文，基于最多289个里德堡原子阵列实现的量子绝热算法，可以高效的解决最大独立集合问题，这是一个NP-hard的优化问题。他们通过理论分析认为此设备的计算速度可以产生平方加速。在实验中，通过与经典算法比较，对于那些最难的问题来说，他们认为已经产生了量子加速优势。基于此系统还可以有很多应用，可以参照这篇理论文章 arXiv:2205.08500 。

里德堡原子阵列技术的关键人物Lukin教授来自俄罗斯，Greiner教授来自德国，Browaeys教授来自法国。美国哈佛大学把Lukin和Greiner招到麾下，才让美国也在此新兴技术中占据了领导地位。虽然Browaeys组最早实现了无缺陷的二维里德堡原子阵列，但这两年其技术发展还是比Lukin&Greiner组稍落后一点。这可能因为哈佛大学对博士生与博士后的吸引力要大得多， 这些天才的年轻人努力工作，极大地促进了技术的进步。

2019年，Lukin&Greiner等人发起成立创业公司QuEra Computing，基于里德堡原子阵列技术开发量子模拟器和量子计算机。2021年QuEra拿到1700万美金的风险投资。在QuEra公司网站上，他们预计到今年底能开发出超过500个原子的可编程量子模拟器，以及64个量子比特的可编程量子计算机，到2024年，可以提供包含1024个量子比特的可编程量子计算机。Browaey教授也在2019年创办了Pasqal公司，推进里德堡原子阵列技术产业化。2022年1月，Nature杂志选出了7项2022年值得关注的新技术，基于里德堡原子阵列的量子模拟技术名列其中。中国科学家们也加入了这个研究领域的攻关。中科院精密测量科学与技术创新研究院詹明生研究团队去年创办了中科酷原科技（武汉）有限公司，并宣布即将发布“汉原1号”中性原子量子计算机。

我一位师弟曾在Lukin组做博后，听说他博后合同到期后就加入QuEra公司负责量子算法理论。前几年我带过的一位本科生，最近听说他从ETH硕士毕业后转去了德国马普所Bloch组，做的方向也是里德堡原子阵列量子模拟与量子计算。由于里德堡原子阵列技术过去几年的迅速发展，吸引了越来越多的人才加入，其未来是非常值得期待的。