Published on September 6, 2025 11:52 PM GMT
“The Delusion of Infinite Economic Growth” is an article published by the Scientific American in 2021, which is one of a long line of pieces making the same argument. They generally all have the same structure:
- Here are one hundred different resources we rely on that at present our consumption of seems to be growing exponentially, but must have a limit. For instance, oil on earth.We acknowledge that techno-optimists will respond with the argument that there may be ways to increase the limit (fracking), or to replace this resource with another with a higher limit (solar).Regardless, exponential curves are magic, and we humans always underestimate how fast they grow. As the SA article puts it, “Exponential growth swiftly, inevitably, swamps anything in finite supply.”And when we reach the limit, bad things happen.1
As a techno-optimist I do indeed want to respond with the argument in (2). Putting imaginary boundaries on systems is a common systems thinking error. “Lithium battery production” isn’t the system, and so its limit is not the limit that concerns us. Our limit is the laws of physics, and the light cone they seem to restrict us to.
But, I must admit their rebuttal to my response in (3) has a certain appeal – exponential curves really do grow very fast. Intuitively, it is true that increasing the limit doesn’t do much in the face of exponential growth. Still, it doesn’t feel like we’re close to any kind of limit. Heck, we aren’t even doing proper fusion yet.
So under the pretense of reviewing this article’s argument,2 I will go through my own analysis to conclude when we reach our limit, when exponential growth must stop. In a sense, this is a steelman of the article they were trying to write, crafted for techno-optimist sensibilities. These are my assumptions.
- The speed of light is absolute.The second law of thermodynamics is correct, i.e. entropy always increases.
For the record, I feel these really are assumptions one needs to explicitly make. Our understanding of physics has last been completely turned on its head just a century ago, and we are going to be discussing the far future. I am assuming the current understanding of physics will never be overturned, in a way that will allow our economy to grow a bit longer. Nevertheless, we must choose some assumptions or leave the current framing entirely, and I choose to accept these constraints.
In the article they briefly touch on recycling, and point out that it too has limits. This is true, but we mustn't leave ourselves with such a qualitative statement. What’s the theoretical maximum ability to recycle? A naive (false) answer would be that E=mc^2, mass-energy cannot be created or destroyed, and so at the limit they are infinitely recyclable. But there’s actually an upper bound to this question.
There’s one thing we know is irreversible, which I hinted to with my assumptions above – entropy always increases, also known as the second law of thermodynamics. Order goes to disorder, and a cloud of hydrogen eventually turns into a black hole. So we can well approximate the maximum entropy of a system with a black hole, which is convenient for our purposes.
So we found some limiter, but how is this a resource we are consuming with an exponential increase in the rate of extraction? Well, we have some amount of entropy in our relevant bubble of the universe right now, and if we rearrange all this matter into a high entropy state (say, a black hole) we get the maximum entropy state.
The amount of entropy we have in our bubble right now is minuscule compared to that black hole, and so we can say that we can increase our entropy by approximately a “bubble black hole” amount. This isn’t a resource – we create more of it, not use it up. But we can call the reverse negative entropy, or as coined by Schrödinger in his 1944 book “What is Life?”, negentropy. That is our resource.3
So the only truly irreplaceable resource is negentropy. And we currently use it as part of everything we do, and the proportion of whatever activity we do that is not reversible is because of its use. The only reason future humanity won't be able to convert matter to energy (E=mc^2), use the energy for our purposes (energy is conserved), convert it back to matter (m=E/c^2), and then repeat the cycle to accomplish infinite work, is because this process increases entropy as a side effect, that is, consumes negentropy. At the end of the day, negentropy is our finite resource, and extending our technology to the limits allowed by our understanding of physics, it is our only truly non-renewable one.
Ok, we did a lot. Abstracting away technological growth to the physical limit, our resource is negentropy, and the limit is when we’ve condensed most of the matter in our bubble of the universe into a black hole. Since it’s hard to fathom why we would actually go all of the way there, imagine we actually have a space station orbiting our supermassive black hole, and our descendents are on it. So our question becomes, how long until they are sitting on that space station, reflecting over the end of our journey of exponential economic growth?
We’re still obeying the initial Scientific American/degrowth framing. Constant exponential growth for X years, up to a collapse at the limit. Now to get years, we need numbers. How much negentropy is humanity consuming, what’s the rate of growth, and what’s the limit where the negentropy reservoir of our light cone is exhausted by our consumption?
The amount of negentropy in our light cone itself depends on how far in the future the limit is reached, because the light cone is constantly expanding. The amount of negentropy it contains grows in spurts, since the amount in every cubic meter of galactic volume really depends on if it is a cubic meter of interstellar medium or a cubic meter of Alpha Centauri. We will simplify things by noticing that regardless of when we reach the limit, our light cone at least includes our solar system, and at most somewhat less than the entire Milky Way.4
Doing some calculations
Entropy is increased through many different things we do, but practically all of it is related to the production and usage of energy. We currently produce half a zettajoule of energy a year (zettajoule = 10^21 joules) and that production is increasing by about 2% a year. A decent approximation (at least when working at log scales) is that all of this energy ends up as waste heat released into the 300K ambient temperature, once we are done with it (or in the case of the alleged 50% of energy we consume which is used directly for heating, that’s precisely what we do with it).
Since dS=dQ/T (the change in entropy is the amount of energy dissipated divided by the temperature of the medium), that’s about 10^41 k entropy added to the universe from human activities in a year, or in our framing, 10^41 k of negentropy is irreversibly consumed (k is the Boltzmann constant). Since it’s related linearly to energy production, it grows like energy production, and so is growing at a rate of 2% year over year. We will assume this rate of growth is constant. If it increases (say because achieving AGI shortens our doubling time) the limit comes closer, if it decreases we no longer have exponential growth.
As for how much negentropy we can potentially harvest, at the lower limit, the mass in our solar system in its maximal entropy state has about as much entropy as a black hole with its mass would have, which is an easy to calculate value given by the Bekenstein-Hawking entropy, about 10^77 k of entropy.
If we take the upper limit of the entire Milky Way galaxy, we just do the same calculation using its mass. Combining both we get a limit of 10^77 - 10^101 Boltzmann constants. Quite a large range, but luckily we are going to be facing this limit off against an exponential.
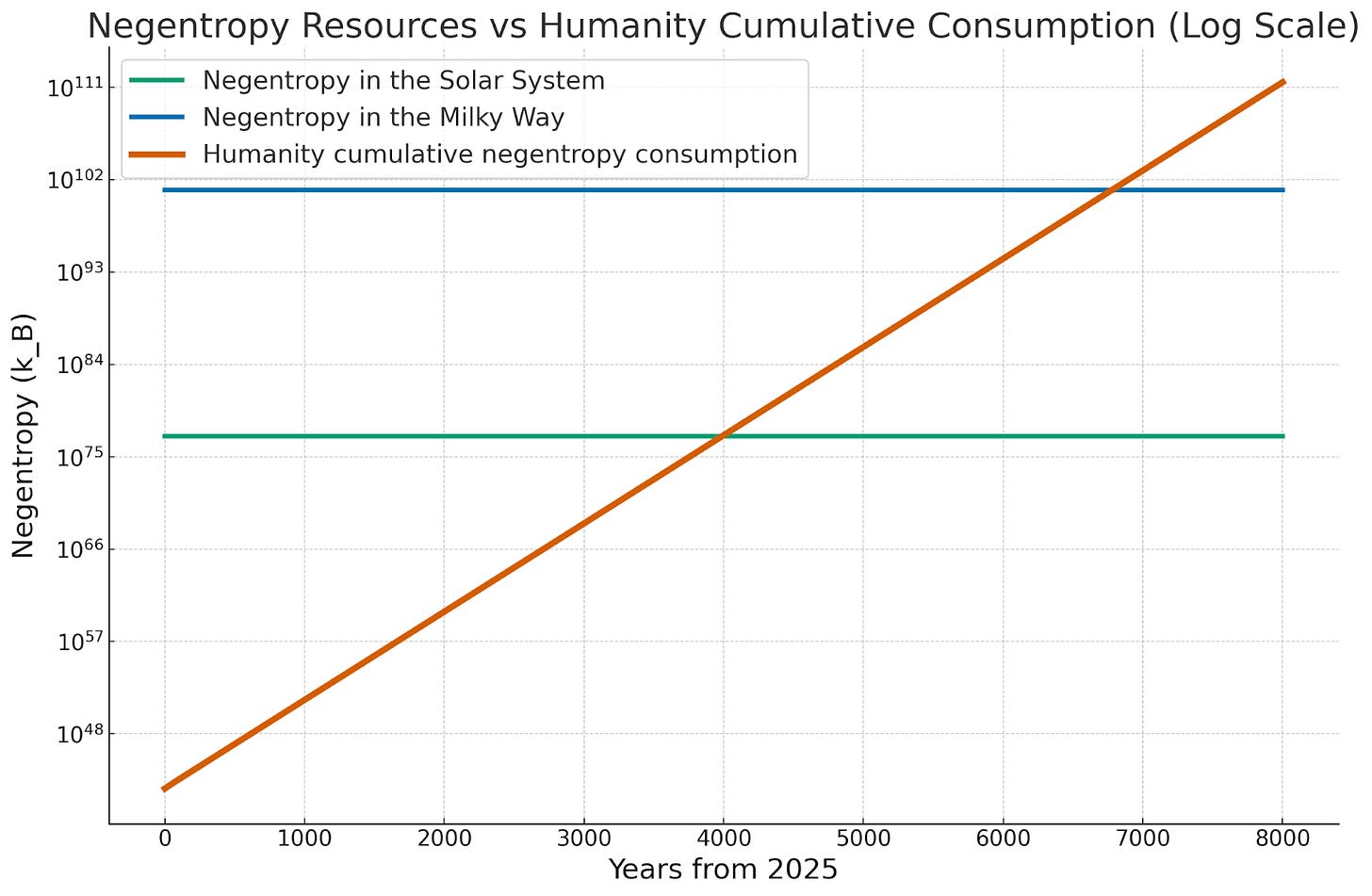
What we get is that assuming our negentropy harvesting rate continues to grow by 2% year over year, we will exhaust the amount available to us in somewhere between 4,000 and 7,000 years. This doesn’t mean our negentropy consumption can’t grow for longer – after all, the light cone constantly expands. But it won’t be able to grow exponentially anymore.
Neither does it mean our economy will no longer grow exponentially, but it does mean that we will be forced to find a way to decouple our economic growth from the creation of entropy. Because of the relation between entropy increase and the usage of energy, that means we’d likely have to decouple economic growth from energy use (indeed, treating mass-energy as a finite resource instead of negentropy shortens the timeline to 1,000-3,000 years). I don’t necessarily think that’s impossible, but I agree that it does place us under some sort of limit, this is at least a different type of economic growth than what we have had so far.
And of course, this is under the above assumption that we don’t discover new physics in the next 7,000 years. I think this calculation shows that while there is certainly truth in the statement that exponentials are fast to meet limits, it is also true that the solar system alone is simply very very big, and we aren’t currently doing all that much to it, to such an extent that it isn’t going to become a true barrier for thousands of years. Our bias to underestimate exponential growth is canceled out by the one to underestimate the sheer scale of the universe.
Regardless of whether you view our limit as the accumulation of pollution or the harvesting of resources, as long as that pollution isn’t entropy and that resource is not negentropy, it relies on the implicit assumption that we fail to increase our efficiency, migrate to a different sort of pollution, or switch to a different type of resource as we approach our limit, something that doesn’t seem to track with recent history, or with techno-optimist priors.
Discuss

