💡 **L0选择不当与重构误差的误导性：** 研究发现，普遍认为的“稀疏度与重构权衡”存在误导。当SAE的L0参数设置低于真实底层特征数量时，即使重构误差表现得更好，学习到的特征也可能是错误的。例如，一个L0=1的SAE在重构上优于一个L0=11的“真实SAE”，但其学习到的特征与真实特征几乎无关，且高度多义性，这与直觉相悖。

🧩 **L0过低导致特征“混合”与多义性：** 当L0被限制得过低，不足以表示输入数据中的真实概念时，SAE会通过混合不相关的特征来“作弊”，以提高重构质量。这种特征混合（feature hedging）的行为破坏了SAE的单义性（monosemanticity），使得每个激活单元（latent）不再代表一个独立的、清晰的特征，而是多个特征的组合。

✅ **正确的L0是学习真实特征的关键：** 研究强调，只有当L0等于底层数据的真实特征数量时，SAE才能正确地学习到所有底层特征。在玩具模型中，当SAE的L0设置为11，与模型中的真实特征数量一致时，该SAE能够完美地匹配“真实SAE”，准确地学习到模型的所有特征，证明了正确L0的重要性。

📊 **“稀疏度与重构权衡”图的局限性：** 传统的“稀疏度与重构权衡”图表，通过比较不同L0下的重构性能来评估SAE的好坏，存在根本性缺陷。它们可能错误地偏好那些虽然重构误差低但学习到了错误、多义性特征的SAE，而忽略了那些虽然重构误差稍高但能够学习到准确、单义性特征的SAE。因此，不能仅凭此图来判断SAE的优劣。

🔍 **寻找正确L0的挑战：** 目前，确定SAE的正确L0仍然是一个挑战。研究人员通常需要训练一系列不同L0的SAE，并进行对比分析。虽然本文未详述寻找正确L0的方法，但指出其在相关研究论文中有提及，并预告了后续将发布相关内容的讨论。

Published on August 26, 2025 4:39 AM GMT

This work was done as part of MATS 7.1. For more details on the ideas presented here, check out our new workshop paper Sparse but Wrong: Incorrect L0 Leads to Incorrect
Features in Sparse Autoencoders.

Nearly all work on Sparse Autoencoders (SAEs) includes a version of the classic "sparsity vs reconstruction tradeoff" plot, showing how changing the L0 (the sparsity) of the SAE changes the reconstruction of the SAE, measured in variance explained or mean squared error. 

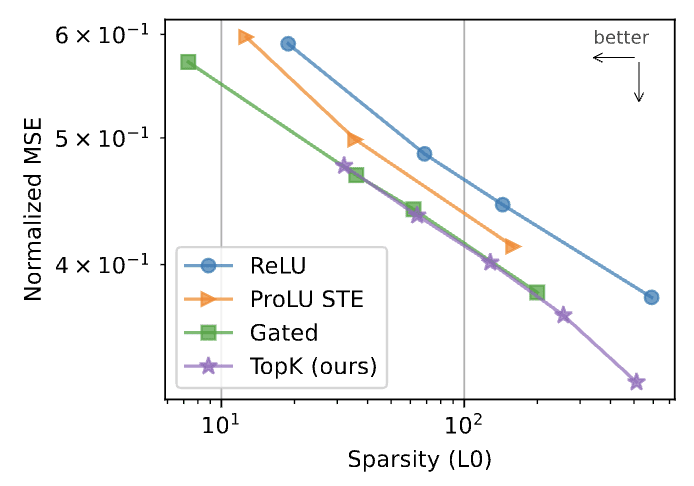
This implies the following two things:

The better the reconstruction the better the SAE. If one SAE reconstructs inputs better than another SAE at a given L0, then the SAE with the better reconstruction score is the better SAE.Any reasonable L0 is equally valid. Decreasing L0 decreases the reconstruction quality of the SAE, but this just a trade-off. There's no correct L0, it's just up to you how much you care about the reconstruction of the SAE.

These assumptions seemed intuitive. All else being equal, an ML model with lower error is better, and it is reasonable to expect SAEs to follow this. Removing constraints on L0 also straightforwardly lets SAEs have lower reconstruction error, and there was no clear reason to pick an L0 over another other than it be "small". To make comparison between SAEs possible at all, researchers simply had to constrain L0.

However, we now believe that both of these assumptions are wrong. In this post, we show via toy model that:

More monosemantic SAEs have higher reconstruction error, when their L0 hyperparameter is smaller than the true underlying L0.The only valid L0 is the true L0 of the underlying distribution, because setting the L0 smaller or larger leads to not reconstructing the true features. 

The idea of a "sparsity vs reconstruction tradeoff" implies an incorrect mental model of how L0 works in SAEs. The implied idea is that as long as the L0 is reasonably low (afterall, they're called sparse autoencoders), then decreasing L0 further should just cause fewer latents of the SAE to fire, but it shouldn't change the dictionary directions of the SAE. Sadly, this is not true. If an SAE is not allowed to fire as many latents as is needed to properly reconstruct the concepts in its input, it can "cheat" by mixing correlated features into its latents, a form of feature hedging. 

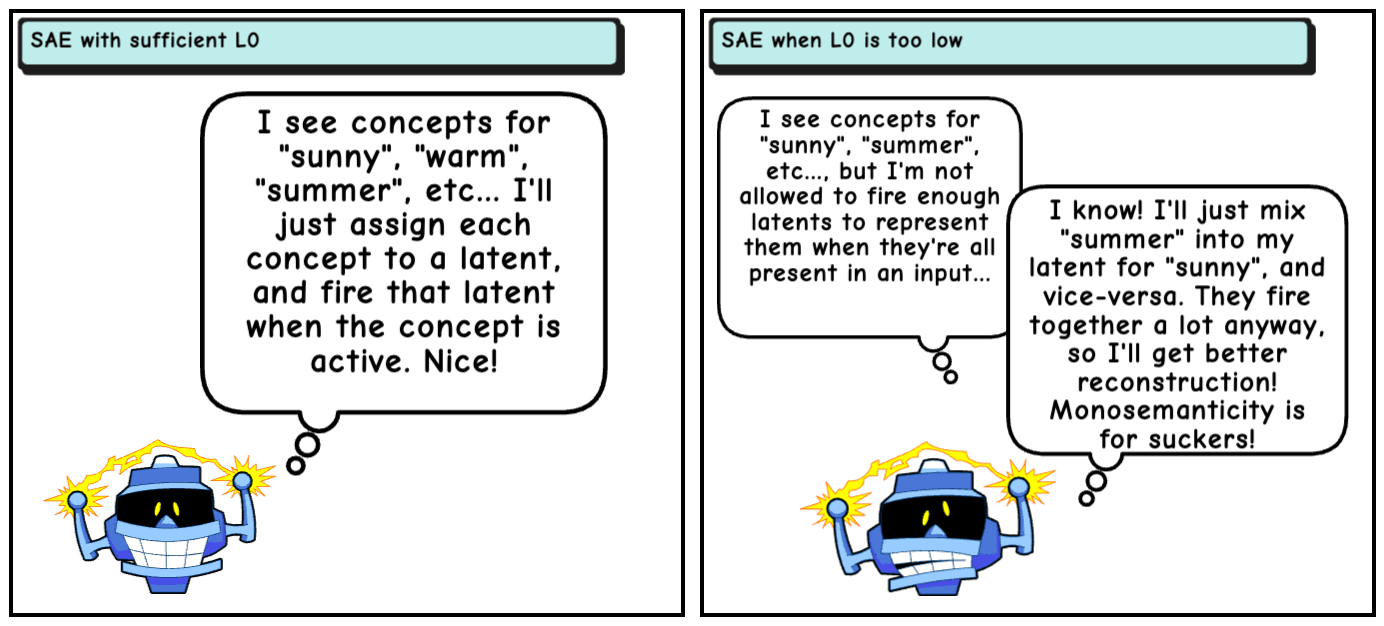
In the rest of this post, we explore this problem in a toy model with correlated features. All code is in this colab notebook.

Toy model of correlated features

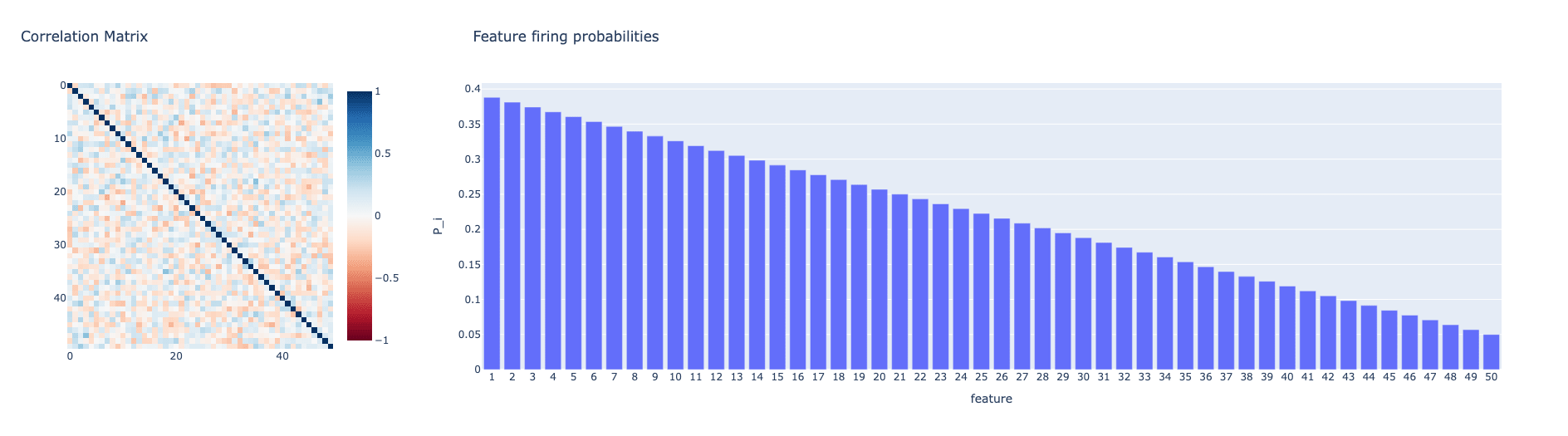
We set up a toy model consisting of 50 mutually orthogonal true features $F=\{f_0,\dots ,f_{49}\}\in R^{100}.$ Each feature $f_i$ has a firing probability $P_i$. We set $P\left(f_0\right)=0.345$, and we linearly decrease each $P_i$ down to $P_{49}=0.05$. These probabilities are chosen so the probability of each feature firing decreases with feature number, and on average ~11 features fire at once. Furthermore, we randomly generate a correlation matrix roughly balanced with positive and negative correlations between features, so the firings of each feature have some correlation with many other features. Each feature fires with magnitude $\sim N(1.0,0.15)$. We create synthetic training inputs for the SAE by sampling true features, and summing all firing features to create a training input. The goal of the SAE, then, is to learn the underlying true features despite only being trained on their summed activations. Since we have ground-truth knowledge of this toy model, we know the true number of features firing in the toy model. We call this the true L0, which is 11 for this model.

Sparsity vs reconstruction

Next, let's train some SAEs with different L0s on this toy model and calculate sparsity vs reconstruction. We'll give our SAEs 50 latents to match the number of true features in our model. Since we know the ground-truth features, we can also create a ground-truth correct SAE by simply setting the the encoder and decoder of the SAE to match the correct features. This SAE, which we'll call the "ground-truth SAE", is the optimal SAE for this toy model, with a dictionary that perfect matches the features of the model. We'll use BatchTopK SAEs for this experiment, since they allow us to directly control the L0 of the SAE and are considered a state-of-the-art architecture. Results are shown below:

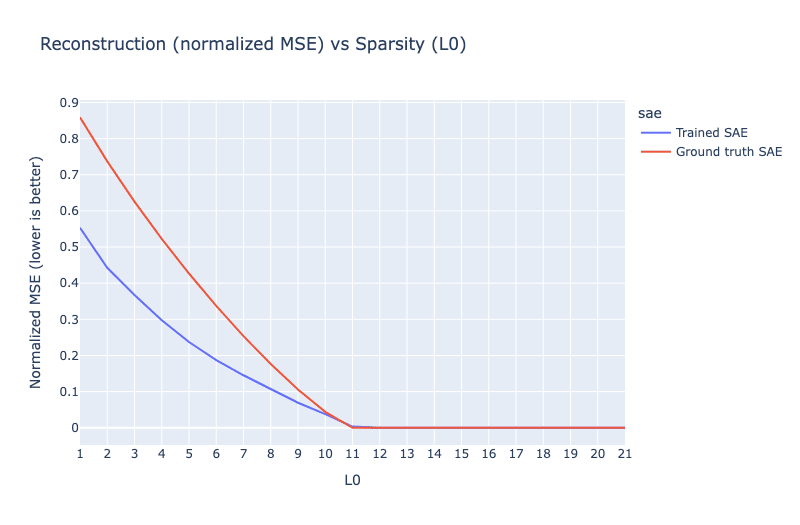
Somehow, our ground-truth SAE, the SAE where we set its latents explicitly to the match the ground-truth features, gets much worse reconstruction than our trained SAEs at low L0! How is this possible? If this were a SAE architecture paper, we would conclude that the ground truth SAE is clearly inferior to the SAE we trained since its sparsity vs reconstruction curve is so much worse. 

Let's look at the SAE we trained compared to the ground-truth SAE, when L0=1. For these plots, we take the cosine similarity between each SAE latent (encoder and decoder) and each true feature vector (both SAE latents and true feature are vectors in $R^{100}$). First, the ground-truth SAE:

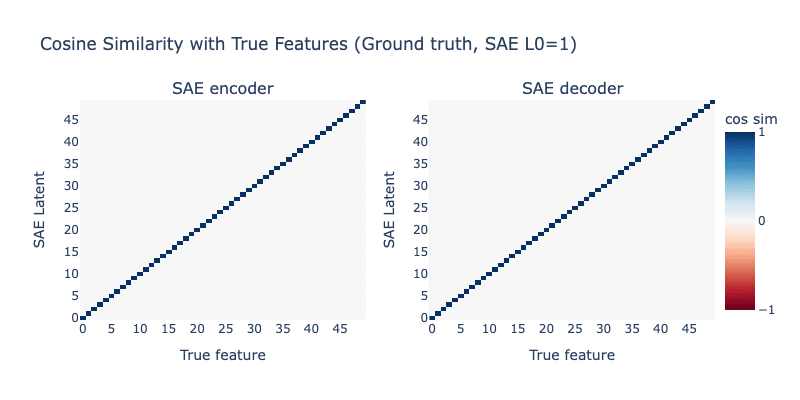
This looks... perfect. We constructed it to be perfect, so this shouldn't be a surprise. Now, let's look at the SAE we trained with L0=1, that achieves much better reconstruction than our ground-truth SAE:

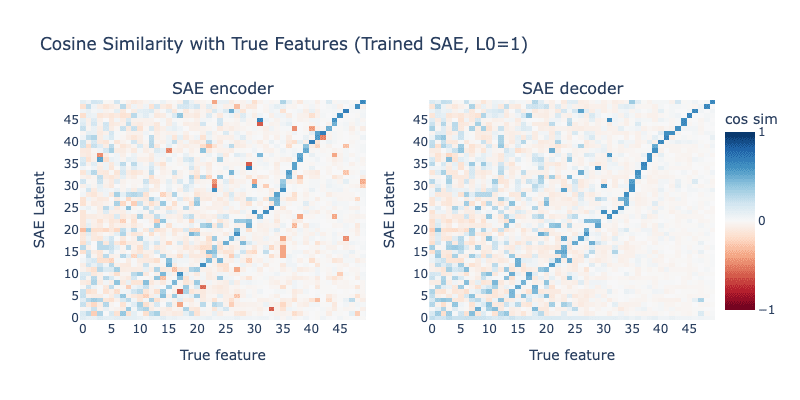
This SAE is a monstrosity. There is virtually no relation between the latents of this SAE and the true features of our toy model, and every feature is very polysemantic. And yet, our "sparsity vs reconstruction tradeoff" plots would claim that this is clearly the better SAE!

Let's check the SAE we trained when L0=11, the correct L0 for the toy model:

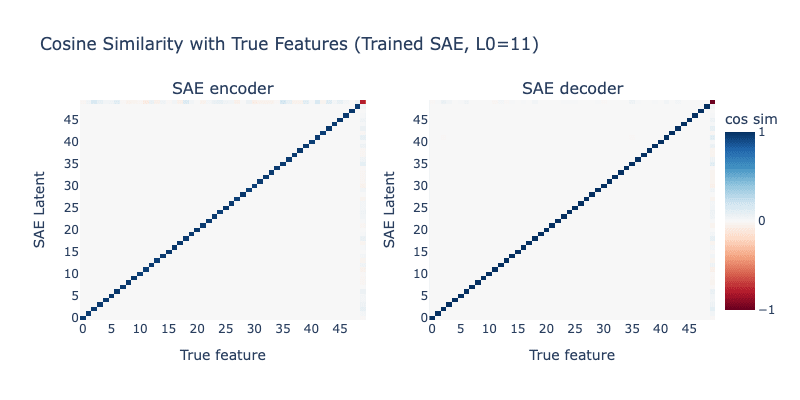
Here the SAE we trained is perfect as well! It exactly matches the ground-truth SAE, and perfectly learns every feature of the toy model. 

Ok, so how can we find the correct L0?

While we won't discuss how to find the correct L0 for a given SAE in this here to keep the focus on sparsity vs reconstruction, we will write a follow-up post with our thoughts on finding the correct L0 for a SAE on this soon. We also cover finding the correct L0 for an SAE in the companion paper,  so take a look at the paper if you're curious!

Discussion

Even in this very simple toy model, we can clearly see that the SAE preferred by sparsity vs reconstruction plots is incorrect when the L0 not picked correctly. Sparsity vs reconstruction plots would lead us to conclude that a correct, monosemantic SAE is clearly worse than an incorrect, polysemantic SAE!

Fundamentally, there is no "sparsity vs reconstruction tradeoff" - if the L0 of the SAE is not chosen correctly, the resulting SAE will be incorrect and polysemantic. If we do not give SAEs enough resources to represent the underlying features of the model by restricting L0, the SAE will react by abusing correlations between features to "cheat" and improve its reconstruction, breaking monosemanticity.