本文探讨了一种检测模型中“特征吸收”现象的新方法。特征吸收是指在训练稀疏自编码器（SAE）时，由于优化目标（如最小化L0范数），原本语义独立的特征被不自然地混合或分离，导致SAE的潜在表示产生“意想不到的空洞”，影响其作为探针的可靠性。文章提出，可以通过寻找那些具有相似因果效应但不同时激活的SAE潜在变量来检测这种现象。理论模型分析了这种方法的原理，并进行了实验验证。然而，实验结果显示，该方法在实践中存在局限性，未能完全区分特征吸收和特征分离，且检测结果的准确性有待提高，需要进一步的研究和改进，例如探索更合适的度量标准和利用LLM生成更具针对性的测试样本。

💡 **特征吸收的定义与影响**：特征吸收是SAE训练过程中出现的一种现象，当模型试图通过混合或分离特征来优化稀疏性时，可能导致原本语义不相关的特征被绑定在一起，或将本应共同激活的特征拆分。这会使得SAE的潜在变量变得不可靠，难以作为理解模型内部机制的准确探针，例如，一个“欺骗性行为”的潜在变量可能实际上是“非周一的欺骗性行为”。

🚀 **检测特征吸收的新方法**：文章提出一种检测特征吸收的理论方法，即寻找SAE的两个潜在变量，它们在对下游层产生因果效应时表现相似，但在实际激活时却很少（或从不）同时发生在同一token上。这种方法利用了特征吸收导致的潜在变量在下游的因果效应具有重叠，但激活模式却相互排斥的特性。

🔬 **理论模型与实验验证**：为了支持该方法，文章构建了一个理论模型，详细阐述了特征吸收的数学表示以及如何通过分析潜在变量的因果效应来检测它。通过在实际模型（google/gemma-2-2b）上进行实验，将一个SAE（𝕬）的潜在变量的因果效应与另一个SAE（𝕭）的潜在变量进行比较，试图量化这种相似性。

⚠️ **实践中的局限性与挑战**：尽管有理论支持，实验结果表明该方法并非万无一失。检测到的潜在变量对可能存在巧合的相似因果效应，或者实际中仍然会共同激活。此外，该方法可能难以区分特征吸收和特征分离，并且现有指标（如效应向量的余弦相似度）与主观判断的特征吸收之间的相关性不够强，这表明需要进一步的研究来改进检测的准确性和鲁棒性。

Published on August 12, 2025 8:46 PM GMT

Summary

This post discusses a possible way to detect feature absorption: find SAE latents that (1) have a similar causal effect, but (2) don't activate on the same token. We'll discuss the theory of how this method should work, and we'll also briefly go over how it doesn't work in practice.

Introduction

Feature absorption was introduced in A is for Absorption.

Their example: Assume the model has two features, 𝒜="this token is 'short'" and ℬ="this word starts with s". In the prompt "Sam is short", 𝒜 activates on "short", and ℬ activates on "Sam" and "short". Hence the L0 across those two features is 3. We train an SAE to recover these features.

But the SAE is trying to minimize L0. So the SAE instead learns latents α and β, where α activates on the token "short", and β activates on all words starting with s, except for "short". (We're treating partial absorption as out-of-scope.)

Hence only α activates on "short", and only β activates on "Sam". Thus L0 across those two latents is 2. The reconstruction is still perfect (see "Feature absorption: Subset case" for why). The SAE has improved on L0, compared to instead using 𝒜 and ℬ as the latents.

Feature absorption is undesirable because it creates surprising holes in SAE latents. 𝒜 and ℬ above don't have a semantic connection. They were only mixed by the SAE optimizer because they happened to co-occur. Feature splitting is easier to predict, e.g. you can a priori predict that a "starts with s" latent will split into "starts with lowercase s" and "starts with uppercase S". But it's harder to predict that a "starts with s" latent won't activate on "short". This makes SAE latents less reliable as probes, e.g. a "deceptive behavior" latent might actually be "deceptive behavior, except not deception on Monday"

A is for Absorption only looked at ground-truth features of the form "starts with x", where x is any letter. This makes it easy to train a linear probe on examples where this feature should be active, and this linear probe gives you the ground-truth for where the corresponding SAE latents should be. But this doesn't work for features in general. You don't know beforehand that the model will have a feature for a topic like "Alaska". For abstract features, it may be harder to generate a training dataset for a linear probe.

Our approach

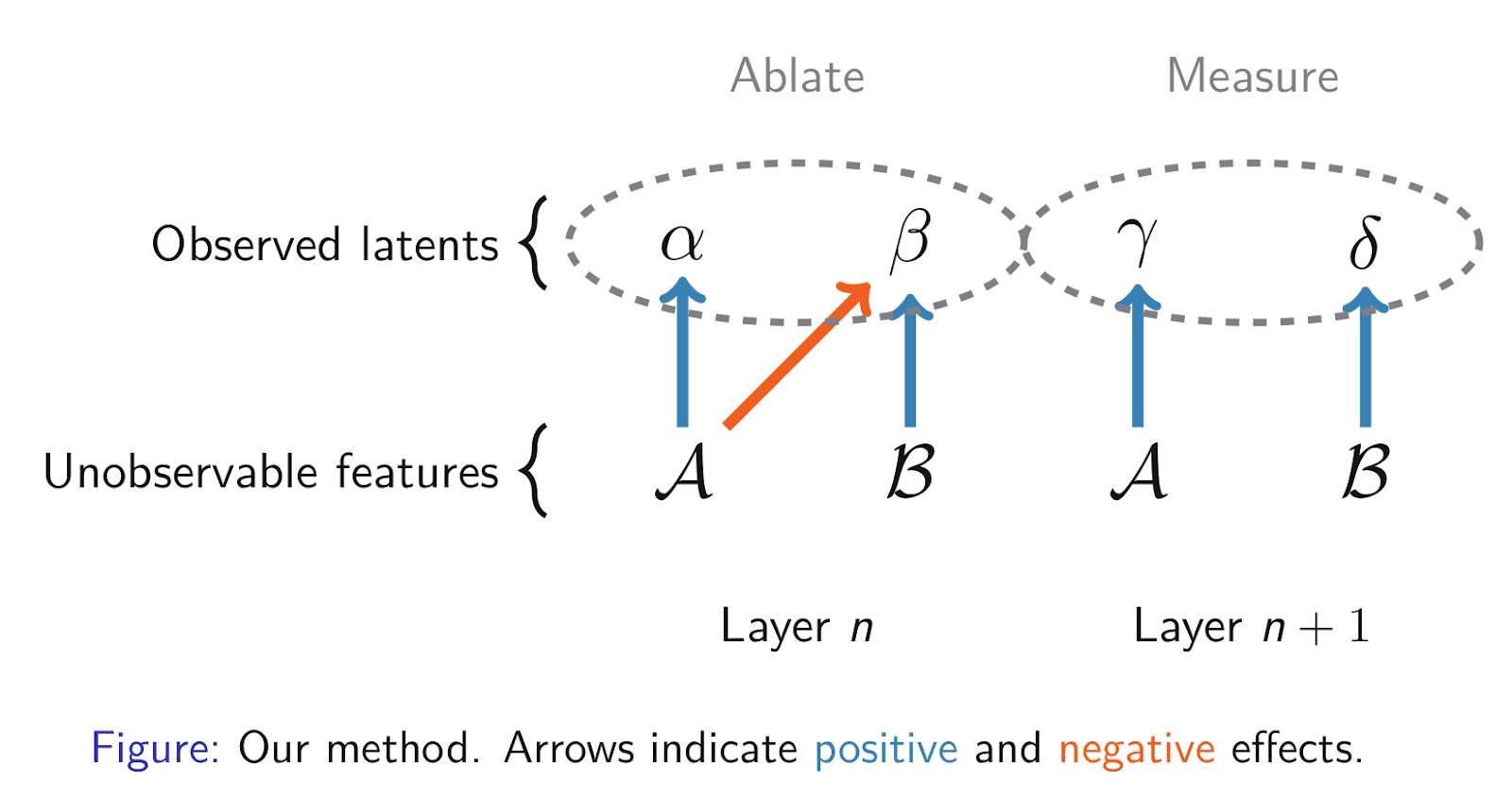
If two latents have been mixed together by feature absorption, they will have similar causal effects on downstream layers, but they won't both occur on the same token. For example, both α and β above influence the model's belief about whether a token starts with s. But α and β never activate on the same token, since gradient descent made them mutually exclusive to reduce L0. This can be used as an automatic way to find feature absorption.

Theoretical model

Let's look at a formal model of feature absorption. This will motivate why our proposed method could find feature absorption.

Conventions

Integers: a, b, c, ...Vectors: 𝐚, 𝐛, 𝐜, ...Tensors: 𝐀, 𝐁, 𝐂, ...Features: 𝒜, ℬ, 𝒞, ...
A feature is a vector in ℝᵈ, where d is the model dimensionWe make the simplifying assumption that features are orthonormalIn reality features are not perfectly orthogonal, and they may have norms different than 1 or 0
Latents: α, β, γ, ...
A latent α is a tuple (αᴱ, αᴮ, αᴰ), where
αᴱ ∈ ℝᵈ is the encoder vectorαᴮ ∈ ℝ is the biasαᴰ ∈ ℝᵈ is the decoder vector
We define a function ℝᵈ → ℝᵈ by 𝐚↦ReLU(𝐚 · αᴱ + αᴮ) αᴰ, where · is the dot productWe use α(𝐚) as shorthand for this function
SAEs: 𝕬, 𝕭, 𝕮, ...
A SAE is also a function ℝᵈ → ℝᵈ, but it can be viewed as a sum of latent functions

Feature absorption: Subset case

There's a more complicated intersection case in the appendix, but the subset case is what we ran experiments on.

Let 𝒜 and ℬ be features such that if 𝒜 is active on a token, then so is ℬ. The intuition is 𝒜 = "this token is 'short'" and ℬ = "this word starts with s" (i.e. the example from A is for Absorption).

Let's define a SAE 𝕬 that has feature absorption for 𝒜 and ℬ. Define latent α with αᴱ = 𝒜 + ℬ, αᴮ = -1, αᴰ = 𝒜 + ℬ. (Informally α "reads from" αᴱ=𝒜 + ℬ and "writes to" αᴰ = 𝒜 + ℬ.) Define latent β with βᴱ = ℬ - 𝒜, βᴮ = 0, and βᴰ = ℬ.

(In a more realistic model, the bias might be small and positive to prevent unrelated features from activating the latent. But we've assumed features are orthogonal.)

We can compare to the "Feature co-occurrence causes absorption" section in Toy Models of Feature Absorption in SAEs. Latent 0 corresponds to β, but latent 3 would correspond to αᴱ = ℬ, αᴮ = 0, αᴰ = 𝒜 + ℬ. We use the version with the nonzero bias here because we'll need a nonzero bias in the intersection case.

Lemma 1: 𝕬 has perfect reconstruction on the features 𝒜 and ℬ. Furthermore, α and β never activate on the same token.

Proof: See appendix.

The central claim is that we can detect this feature absorption by looking at downstream effects on a later SAE 𝕭. Heuristic argument:

Choose 𝕭 close enough to 𝕬 so that 𝕭 can still read the features 𝒜 and ℬ. Since feature absorption is a reparametrization of the features, we don't want to confuse that with actual computation happening to the features. So we want 𝕬 and 𝕭 to be close together. The best 𝕭 might be an SAE trained on the same layer with a different seed.

Say a latent γ in 𝕭 reads from 𝒜, and a latent δ in 𝕭 reads from ℬ. Then ablating α will affect γ and δ (as αᴰ = 𝒜 + ℬ), but ablating β will only affect δ (as βᴰ = ℬ).

Note that we can't directly ablate 𝒜 and ℬ because we can only manipulate latents, not features.

Hence if we actually run this ablation experiment, we will notice that α and β have a shared causal effect: all latents δ in 𝕭 that are affected by β will also be affected by α. But there will also be a latent γ in 𝕭 that is affected only by α and not β. This experiment can be run many times with different α and β to search for an α and β satisfying these conditions.

This method isn't watertight. If 𝕭 has the same feature absorption as 𝕬, this method won't work. Intuitively, if it did work, we could discard 𝕭 and use 𝕬 to find feature absorption in 𝕬. (See appendix for a longer argument.)

But in practice we hope that 𝕭 is sufficiently different than 𝕬. SAEs are known to be sensitive to seed.

Methods

See the methods section in the appendix for details on how we operationalize the theory. In particular, we measure amount of shared causal effect by looking at the cosine similarity of the effect vectors (where an effect vector has as many elements as 𝕭 has latents).

Results

Ideally, the metric of "does this pair of non-co-occurring latents have similar effects when ablated" would have a strong positive correlation with "does this pair of latents subjectively look like feature absorption if you try a few prompts".

That is not currently the case.

Failure modes:

The script outputs two latents that don't seem related
Hopefully more data would fix this, since the causal effects may have been similar by coincidence
The script outputs two latents, but they actually do co-occur if you try making up a prompt to test this
More data might not fix this, since the co-occurrence data is already based on ~1e6 promptsIt could be possible to use an LLM to generate synthetic prompts where the two latents could co-occur
If the candidate latents are "starts with e" and "is related to pachyderms", ask Claude to write a prompt where there's a word that is both of those things. Hopefully Claude figures out that "elephant" is such a word. Then we can automatically test if both latents activate on "elephant"
The script outputs two latents that are both single-token latents
e.g. suppose there's a latent for the token "Barack" and a latent for the token "Obama" (if these are indeed tokens)Then these will never co-occur, but they'll have similar causal effects
We want a metric that separates out the latent pairs with feature absorption. Hence when we plot the cosine similarity of the effect vectors for various pairs, we hope to see two modes. But the histogram turns out to not be bimodal. And it's possible to cherry-pick examples that subjectively look like feature absorption from both ends of the distribution. Hence this metric isn't strongly correlated with feature absorption.

Future work

Look at toy models of feature absorption and feature splitting. Perhaps there's some property that only one of them satisfies, which we can use to filter out feature splittingThe current script's ablations are slow. It might be possible to replace them with an approximation using gradient attribution.Cosine similarity of the effect vectors might not be the best way to compute shared causal effects. Perhaps another metric like Jaccard index would do better.

Author contributions

TE led the project, ran the experiments, and drafted the paper. LRS provided research mentorship, developed the theoretical model of feature absorption, and suggested code optimizations. CLA provided research management, technical advice, and paper feedback.

Acknowledgments

The Pivotal Research Fellowship funded TEAlex Spies had multiple meetings with TE to discuss debugging and paths forward.David Chanin reviewed a draft and gave feedback on a poster presentation.Dan Wilhelm reviewed a draft.Tilman Räuker gave feedback on a poster presentation.Pivotal's other technical fellows listened to early presentations of this work and gave feedback. In alphabetical order, they are Philipp Alexander Kreer, Trevor Lohrbeer, Jord Nguyen, Avi Parrack, and Aaron Sandoval.

Appendix

Proof of Lemma 1

We can calculate the outputs of the latents, given various combinations of features as inputs.

For instance, we have α(𝒜 + ℬ) = ReLU((𝒜 + ℬ) · αᴱ + αᴮ) αᴰ. As features are orthonormal, this simplifies to ReLU(2 + -1) αᴰ = αᴰ = 𝒜 + ℬ.

Similarly we can calculate β(𝒜 + ℬ) = 0.

Thus 𝕬(𝒜 + ℬ) = α(𝒜 + ℬ) + β(𝒜 + ℬ) + other latents that don't activate = (𝒜 + ℬ) + 0 + ... = 𝒜 + ℬ

Likewise we have 𝕬(ℬ) = α(ℬ) + β(ℬ) + other latents that don't activate = (0) + (ℬ )+ ... = ℬ

The case 𝕬(𝒜 ) isn't possible because the tokens on which 𝒜 activates are a subset of the tokens on which ℬ activates.

For the second part of the lemma, observe that in the above calculation α(𝐚) was zero if and only if β(𝐚) was nonzero. ∎

What happens if 𝕭 has the same feature absorption as 𝕬?

This is the subset case.

This means that 𝕭 has a latent ε with εᴱ = 𝒜 + ℬ, εᴮ = -1, and εᴰ = 𝒜 + ℬ, as well as a latent ζ with ζᴱ = ℬ - 𝒜 , ζᴮ = 0, and ζᴰ = ℬ. We further assume that ε and ζ are the only latents in 𝕭 that read from 𝒜 or ℬ.

Suppose we ablate α. This changes αᴰ = 𝒜 + ℬ to 0 in 𝕬's output, i.e. 𝕭's input. Previously we had ε(𝒜 + ℬ) = 𝒜 + ℬ, and also ζ(𝒜 + ℬ) = 0 (see proof of Lemma 1 for calculations). After the ablation, we have ε(0) = 0, and ζ(0) = 0. So ablating α affects ε but not ζ.

Suppose we ablate β. This changes βᴰ = ℬ to 0. But in order to ablate β, β must have been active. Hence 𝒜 cannot have been active, as it would prevent β from activating. Thus before the ablation, ε was not active, since it requires 𝒜 to be active. After the ablation, ε is still not active, as ε(0)=0. Meanwhile, ζ changes from ζ(ℬ) = ℬ to ζ(0) = 0. So ablating β affects ζ but not ε.

Hence α and β no longer have a shared causal effect, i.e. there is no single latent in 𝕭 that will deactivate if we separately ablate both α and β. Thus our method won't find a connection between α and β.

Feature absorption: Intersection case

This section is inspired by the "undesirable feature splitting" example in Figure 4 of Ayonrinde et al.

Let 𝒜 and ℬ be features such that neither is a subset of the other. Sometimes they co-occur, sometimes only one appears, and mostly neither appears (features are sparse).

As intuition, 𝒜 might be "deception", and ℬ might be "Monday". We want the SAE to find latents for those features. But to maximize sparsity, the SAE might instead learn the less useful latents α="deception but not on Monday", β="Monday except in the context of deception", and γ="deception on Monday".

Let's define a SAE 𝕬 that exhibits feature absorption for these features. Specifically, define three latents:

α with αᴱ = 𝒜 - ℬ, αᴮ = 0, αᴰ = 𝒜 (reads from "A but not B" and writes to A)β with βᴱ = ℬ - 𝒜, βᴮ = 0, βᴰ = ℬ (reads from "B but not A" and writes to B)γ with γᴱ = 𝒜 + ℬ, γᴮ = -1, γᴰ = 𝒜 + ℬ (reads from the intersection and writes to the intersection)

Lemma 2: 𝕬 has perfect reconstruction on the features 𝒜 and ℬ. Additionally, no two of α, β, and γ ever activate on the same token.

Proof: Similar to the proof of Lemma 1, calculate 𝕬(𝒜), 𝕬(ℬ), and 𝕬(𝒜 + ℬ). ∎

Again, we can detect this feature absorption by examining the causal effects in a downstream SAE 𝕭. Heuristic argument:

Let's say in 𝕭 we have:

Latent δ that reads primarily from 𝒜 (specifically the part unique to 𝒜)Latent ζ that reads both from 𝒜 and ℬLatent η that reads primarily from ℬ (specifically the part unique to ℬ)

Effects of ablating the latents in 𝕬:

Ablating α will affect δ and ζ because they read from 𝒜Ablating β will affect ζ and η because they read from ℬAblating γ will affect all of δ, ζ, and η.

Hence α and β will have a shared causal effect (ζ), but each of α and β will affect a downstream latent that the other does not.

Methods

Choose a model, in our case google/gemma-2-2bChoose a SAE 𝕬 with a latents from Gemma Scope
This is the SAE where we will look for feature absorption
Choose a later SAE 𝕭 with b latents from Gemma Scope
This is the SAE where we will measure the effect of ablating latents in SAE 𝕬We used 𝕬=Layer 20 MLP, 𝕭=Layer 21 residual
Choose some dataset of prompts
We used https://huggingface.co/datasets/monology/pile-uncopyrightedRoom for improvement: Use the dataset that the SAE was trained on?
For each prompt in the dataset:
For each latent in SAE 𝕬:
Ablate that latent on the whole promptMeasure the effect on all the latents in SAE 𝕭, on the final token onlyRoom for improvement: Average the effect on all tokens? Only measure the effect on the immediate next token (or on this token)?
Hence obtain a tensor 𝐓 of shape (a, b), where element 𝐓(i, j) is the total causal effect of SAE 𝕬's latent i on SAE 𝕭's latent j
i.e. the change in j when i is ablated, summed across all prompts where i is ablated
Look for pairs of latents in SAE 𝕬 (i.e. α₁, α₂ ∈ {1, 2, ..., a}), sorting by similar causal effect
To measure how similar the causal effect is, get the corresponding rows 𝐓[α₁] and 𝐓[α₂], and then take the rows' cosine similarityNotation: For this pair, we call 𝐓[α₁] and 𝐓[α₂] the effect vectors
Exclude any pairs of latents that ever both activated on the same tokenThis process should generate pairs with feature absorption

Code is here

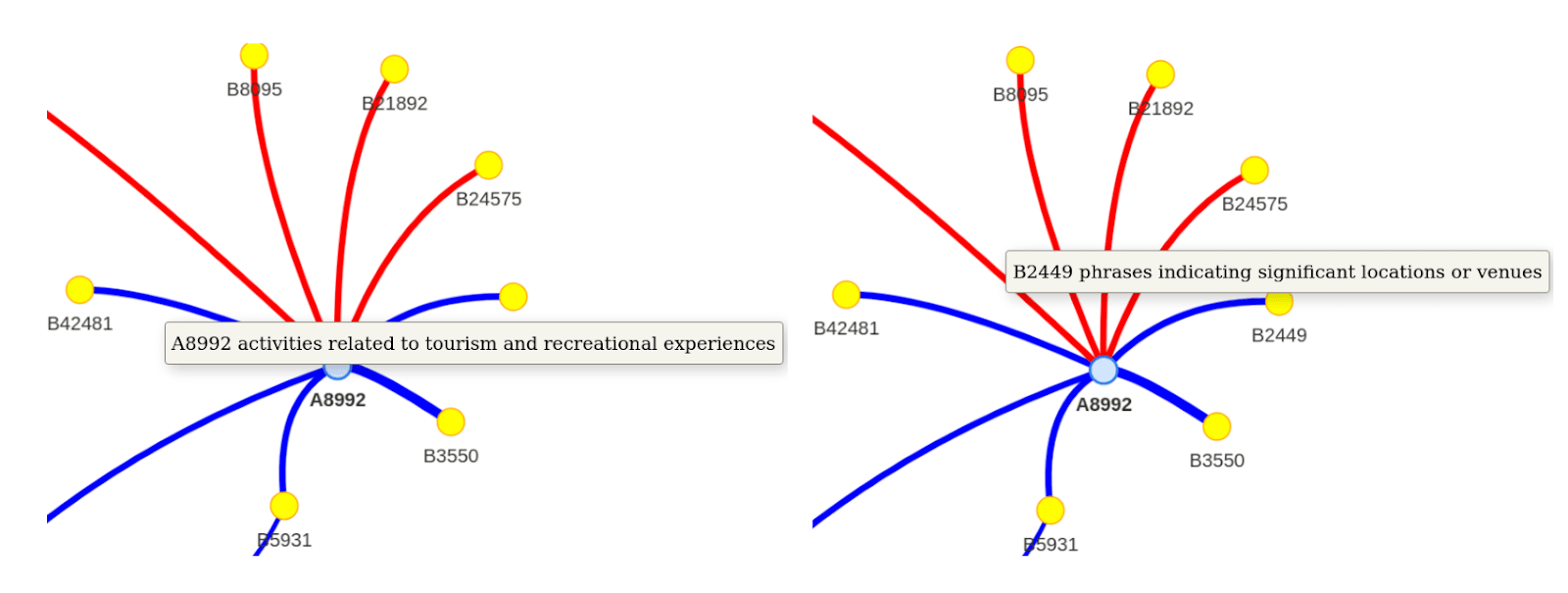
Sanity check

As a sanity check, we can look at the strongest causal links (i.e. the largest positive and negative values from 𝐓) to see if they make sense. See here for a visualization (or see the screenshot for a non-interactive visualization). Indeed, the edges mostly connect latents that have plausibly related meanings.

We labeled latents in SAE 𝕬 with an A and colored them blue, and we labeled latents in SAE 𝕭 with a B and colored them yellow. Blue edges are a positive causal effect; red edges are negative.

Discuss