本研究调查了Meta的SONAR文本自动编码器是否在不同领域（语言语法、数学、代码、棋类）中隐式学习“正确性”。研究发现存在明确层级：代码有效性（96%准确率）> 语法正确性（93%，跨语言）> 基本算术（76%，仅加法）> 棋类句法（弱）> 棋类语义（缺失）。层级表明正确性源于压缩效率而非显式推理，有效结构比随机噪声更容易编码/解码，但不需语义意义。研究使用PCA可视化和逻辑回归探针，结果显示模型在代码和语法上表现最强，但在棋类领域缺乏深层理解，暗示AI安全评估需关注模型隐式能力。

🔹代码有效性：SONAR在Python代码正确性检测上表现最佳（96%准确率），通过PCA和逻辑回归探针清晰分离合法与非法代码，表明模型能识别符合压缩效率的有效结构。

🔹语法正确性：模型展现跨语言语法理解能力，对英语语法探针权重能成功分类其他语言句子，说明其捕捉到的是通用句法模式而非特定语言规则。

🔹算术能力有限：在数学正确性检测中，SONAR仅对简单加法（76%准确率）表现出微弱理解，对乘除法等复杂运算表现不佳，反映其推理能力受限于训练数据模式而非逻辑能力。

🔹棋类领域缺失：模型对棋类句法（合法走法）仅呈现弱且依赖非法走法数量的信号，语义层面完全缺失，未发现棋盘状态内部表征，显示其缺乏对抽象规则的深层认知。

🔹压缩效率主导：研究提出解码器效率假说，认为正确性理解源于有效结构的可压缩性，而非显式训练，暗示模型能力更多由架构和数据决定而非抽象推理发展。

Published on August 6, 2025 12:13 PM GMT

TL;DR: We probed SONAR text autoencoders to see if they implicitly learn "correctness" across domains. Turns out they do, but with a clear hierarchy: code validity (96% accuracy) > grammaticality (93%, cross-lingual) > basic arithmetic (76%, addition only) > chess syntax (weak) > chess semantics (absent). The hierarchy suggests correctness emerges from compression efficiency rather than explicit reasoning. Valid structures are easier to encode/decode than random noise, but don’t need to make semantic sense. 

---

ARENA Context

This research was completed during the final week of ARENA 5.0 bootcamp. Despite some technical hiccups, we each invested roughly 4 days into this project. Goals: a) showcase our work, b) highlight ARENA's value, and c) make a genuine (if small) contribution to mechanistic interpretability. Anton and I did a small-scale MechInterp project on the internal embeddings of SONAR, a text autoencoder by Meta, following up some initial work by NickyP.  Anton focused on the language manifold in SONAR, while I focused on investigating the degree to which SONAR encodes correctness. Anton’s contribution can be found here (link following soon).

Abstract

We investigated whether SONAR text autoencoders develop internal representations of "correctness" across multiple domains: language grammaticality, mathematical validity, code functionality, and chess legality/semantics. SONAR text autoencoders function by encoding text into a fixed-size sentence embedding using a Transformer-based encoder and then reconstructing the original text from this embedding with a corresponding decoder. Using PCA visualization and logistic regression probes, we found a clear hierarchy of correctness understanding, with strongest signals in code validity and language grammaticality, yet no signal for more complex reasoning domains.

Introduction and Motivation

Research Question: Do text autoencoders implicitly learn concepts of "correctness" to aid reconstruction?

Hypothesis: Since autoencoders compress sequences into sentence embeddings for reconstruction, maintaining correctness information should facilitate better decoding. If you're trying to reconstruct something from a compressed representation, knowing it follows certain rules makes the job easier.

Domains Tested:

Grammaticality (across languages)Mathematical correctness (arithmetic)Code validity (Python functions)Chess legality and semantics

Our approach was admittedly limited. We used the same two hammers (PCA + logistic regression) for every nail we encountered. But sometimes simple tools reveal interesting patterns.

Why is this relevant for AI Safety? SONAR isn't a scary model, but that's exactly why it's useful. It's a transformer-based model organism that lets you do mechanistic interpretability work without melting your GPU or your budget. More importantly, understanding "agent overhang", how much reasoning capability is lurking in models, is crucial for estimating risks in larger systems.

Moravec's paradox applies here: a language model's learning curriculum doesn't mirror human development. What seems "easy" to us might be hard for the model, and vice versa. The hierarchy we found (code > grammar > arithmetic > chess) doesn't follow intuitive difficulty rankings. This matters because if we can't predict capability emergence in simple models, we're flying blind with larger ones.

Even "stupid" models can surprise you. Understanding their exact capabilities isn't just academic. It's practice for the harder problem of interpreting systems that actually matter for safety. 

The compression efficiency explanation also has implications: if correctness emerges from compression rather than explicit training, then capability might be more predictable from architectural and data choices than we think. Or it might be less predictable if compression dynamics are chaotic. Either way, we need to find out on models we can actually understand.

Methodology

Model: SONAR text autoencoder

I will refrain from explaining the SONAR model’s architecture; there is already a great write-up on this on LessWrong. We utilized the same “hammer” for all of the following experiments:

Extract sentence embeddings for correct/incorrect examplesVisualize with PCA for linear separabilityTrain logistic regression probes for classificationTest cross-domain generalization

The core idea: if the model stores correctness information, we should be able to extract it from the internal representations, and use it to linearly predict correctness from the embeddings.

Results

Grammaticality: The Foundation

Initial Experiment: Fed random sentences vs grammatical sentences into the model, then applied PCA. Clear separation emerged, but this wasn't representative. Random text isn't the same as ungrammatical text.

Refined Experiment: Created pairs of grammatical and ungrammatical sentences, where the latter were generated by jumbling word order of the former. This controlled for vocabulary and content while isolating grammaticality.

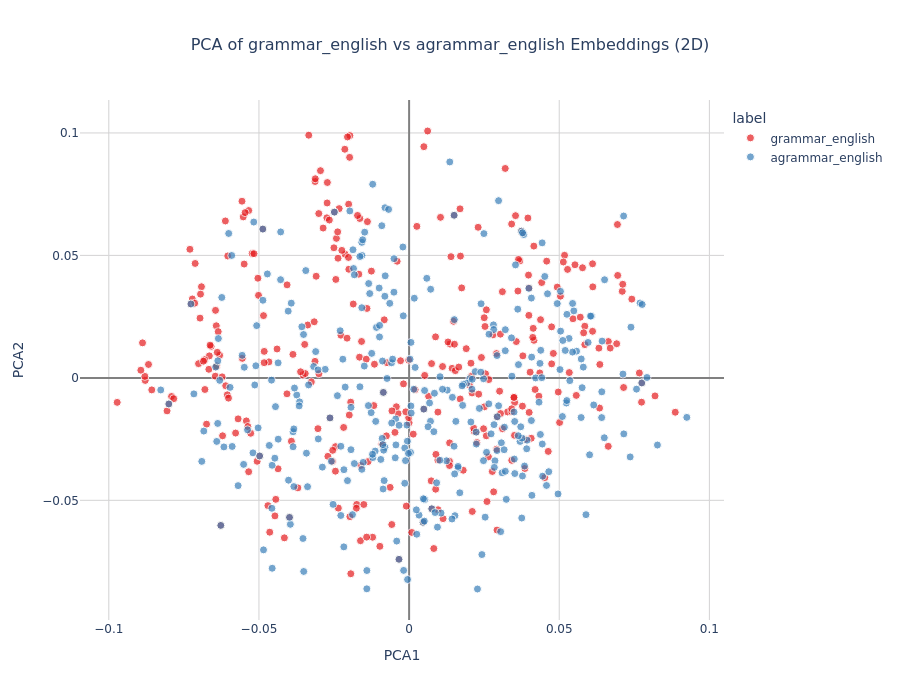
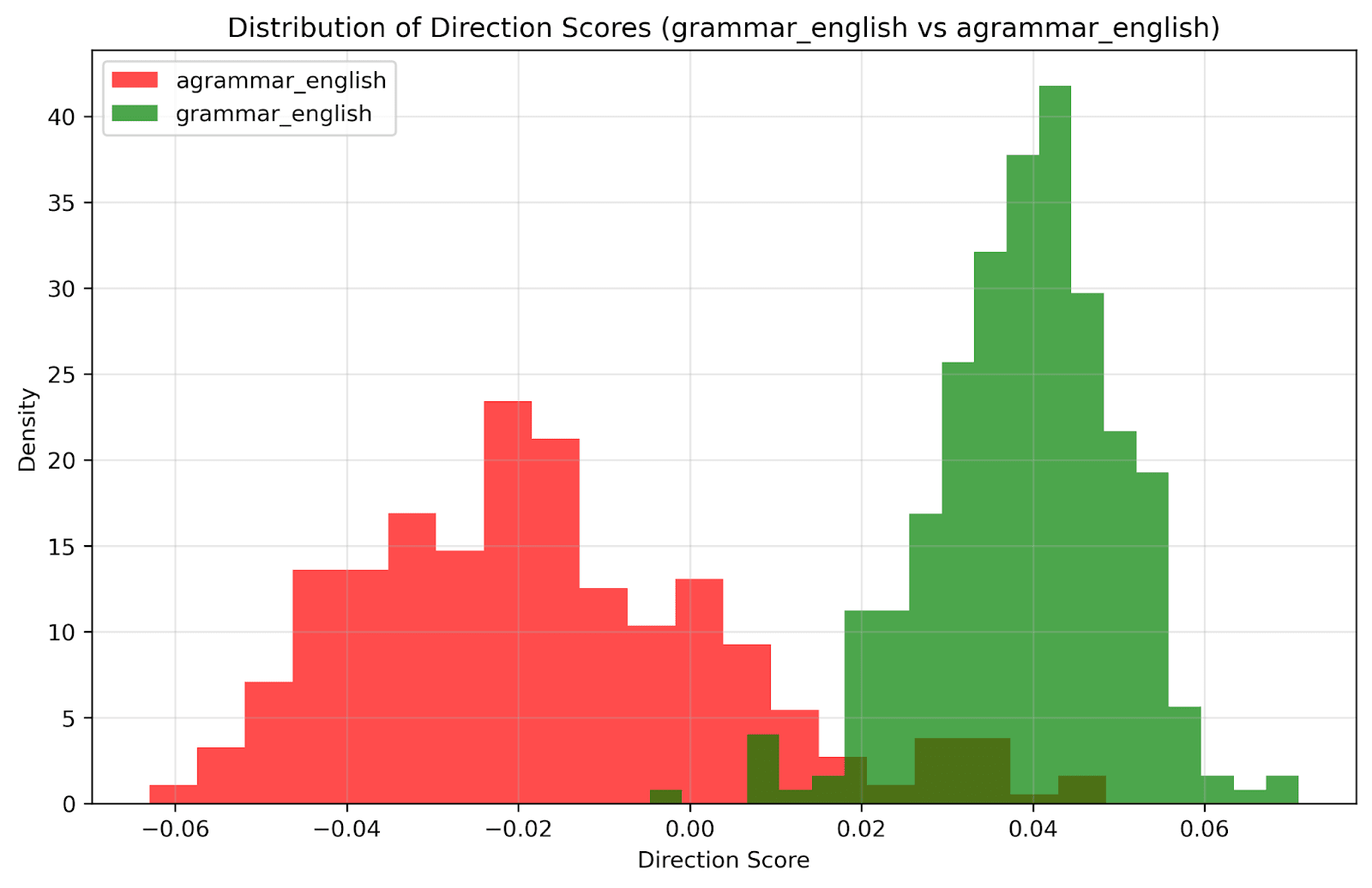
Results:

No clear linear separation with PCA aloneLogistic regression achieved 94% train, 93% test accuracyCrucially: The same grammaticality direction, extracted from the logistic regressor weights, held across languagesWeights from English grammaticality probes successfully classified grammaticality in other languages

Interpretation: The model develops language-agnostic grammaticality representations, suggesting it captures universal syntactic patterns rather than language-specific rules.

Mathematical Correctness: Limited Scope

Next up, we investigated how far this “grammaticality”-understanding goes. We asked ourselves: How much does the model actually "reason" about its encodings? Does it go beyond surface-level language patterns to something resembling logic?

Experiment Setup: Trained logistic regressors on sentences like "The result of X + Y is Z" where Z was either correct (X + Y) or incorrect (random number).

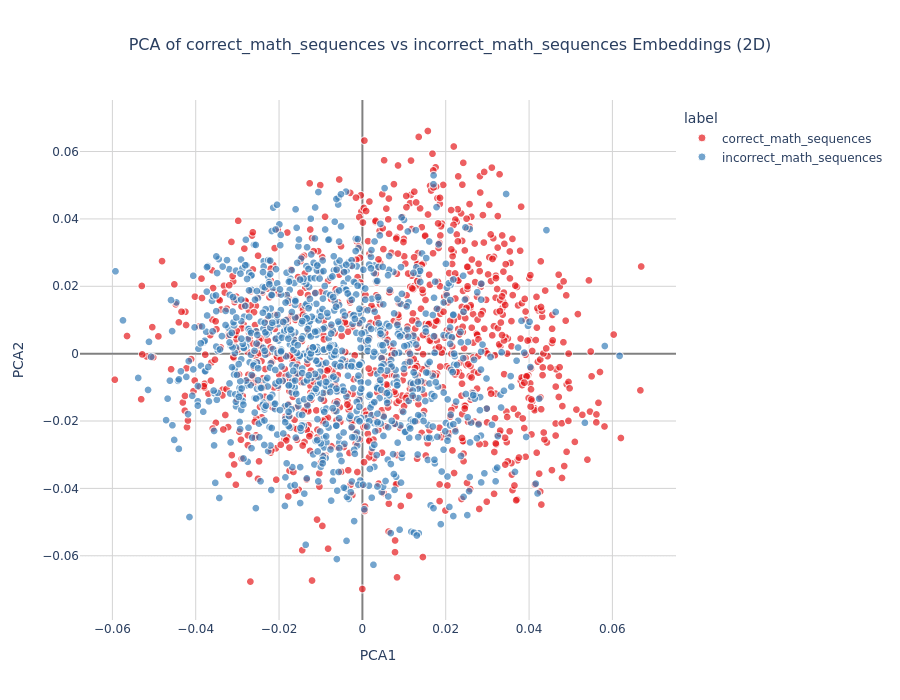
Results:

Addition: 80% train, 76% test accuracyMultiplication: Below chance performanceSubtraction: Below chance performance

Interpretation: The model shows limited mathematical understanding, primarily for simple addition. This likely reflects training data patterns rather than genuine arithmetic reasoning.

Code Validity: Strongest Signal

Setup: Tested uniformly named Python functions where some produced valid "Hello World" output while others contained runtime errors (division by zero, syntax errors, etc.).

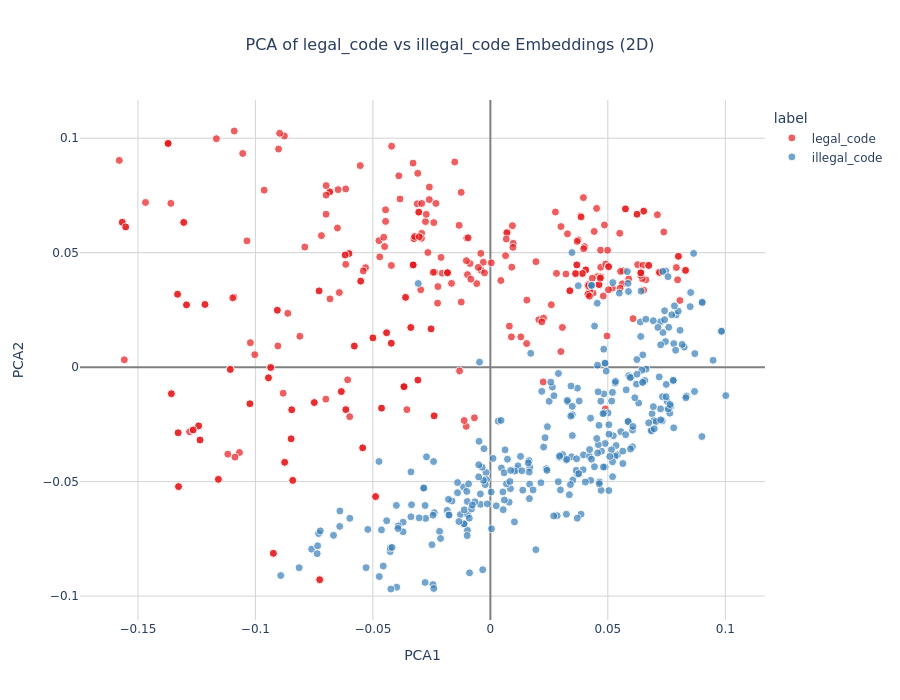
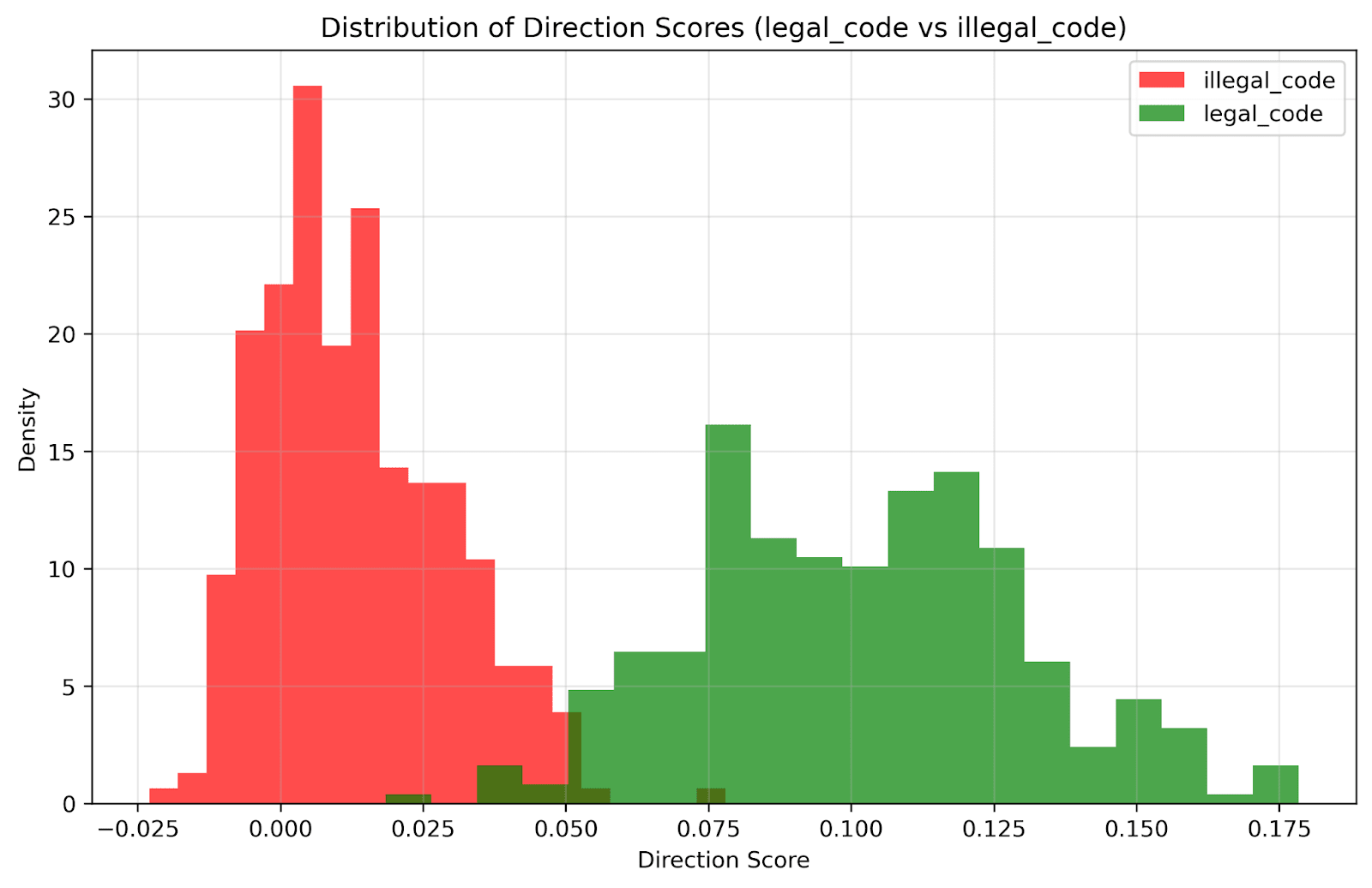
Results:

PCA showed clean separation between valid and invalid codeLogistic regression: 98% train, 96% test accuracyStrongest correctness signal we observed

Here we formulated our main hypothesis:

Decoder Efficiency Hypothesis: Valid code patterns may be fundamentally easier to reconstruct than syntactically/semantically broken code. Valid structures follow consistent rules, making them more compressible. The model likely develops shortcuts for common valid patterns.

One can see this as proof of Kolmogorov Complexity in the wild.

Chess: Syntax vs Semantics

Lastly, we wanted to venture into realms of SONAR’s training test corpus that are harder to approximate using N-Grams, to see if our results so far are product of a sophisticated pattern matcher, or something more akin to genuine understanding.

First, we investigated whether we can predict from the internal embeddings whether a playout of a Chess game is legal (according to the rules of Chess itself). Importantly, we did not test whether we can predict whether a random string is in PGN notation, but rather whether a seemingly legal playout in PGN notation is legal. Therefore, this requires understanding of the rules of chess, i.e. knowing that a pawn cannot move three squares.

Also, an important distinction is that these playouts were randomly generated. From all possible playouts of Chess games, only a few are contained in SONAR’s training test corpus. By using randomly generated chess games, we ensure this is not approximatable by an N-Gram approximator.

Syntactic Experiment: Generated random chess games in PGN notation, then introduced illegal moves. Tested whether embeddings could distinguish legal from illegal move sequences.

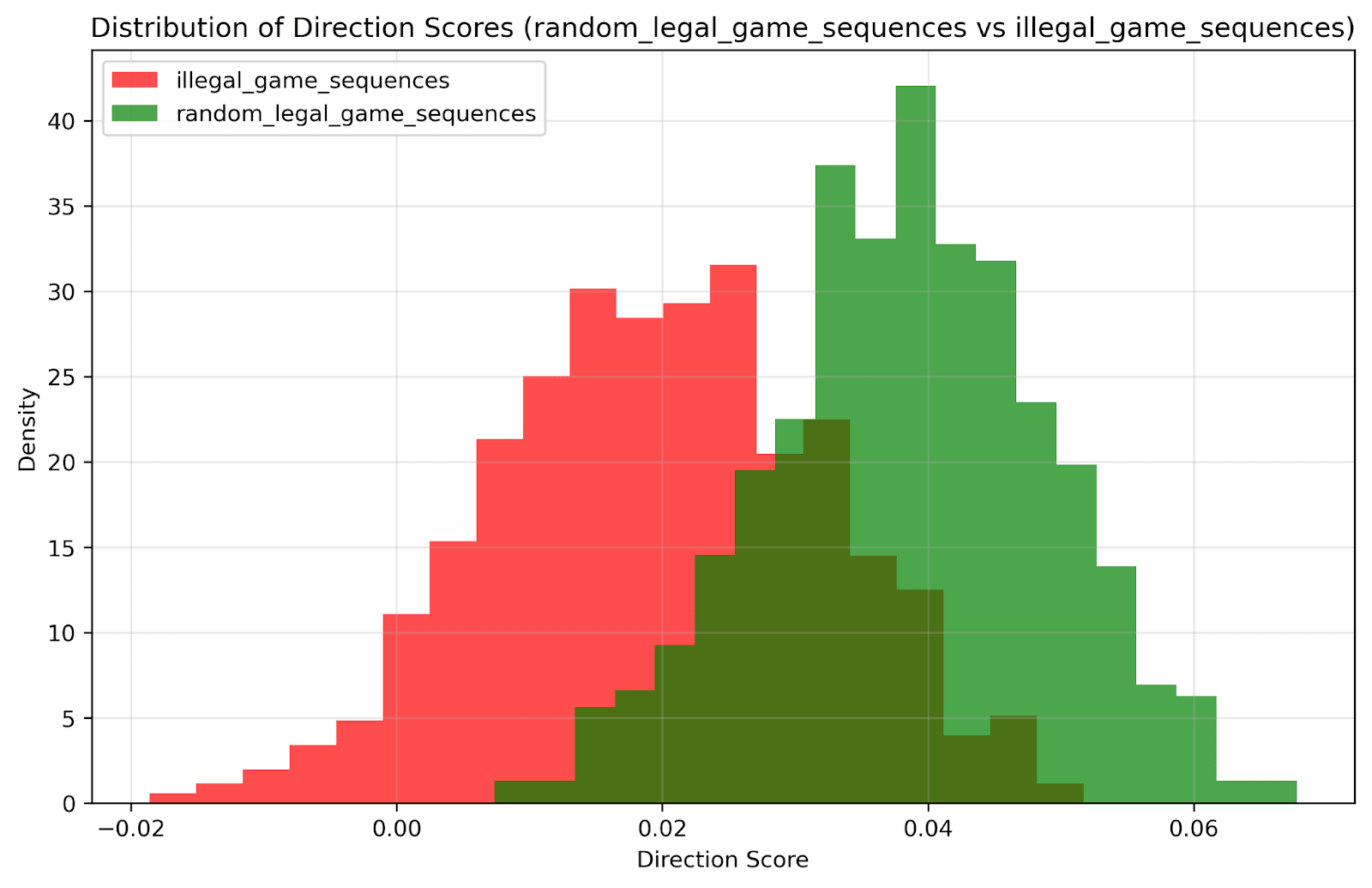
Results:

No clear PCA separation for legal vs illegal gamesLogistic regression accuracy correlated with number of illegal movesMore illegal moves → better classification accuracySuggests weak sensitivity to chess syntax, but not robust understanding

To test this further, we checked whether we can probe for board state features directly. This tests whether the model is not just checking the syntax of PGN notation, but is checking the syntax by having an emergent world representation of the board game.

Semantic Experiment: Probed directly for board state features after observing game sequences. Attempted to predict:

Whether white queen remains on boardPiece advantageOther positional features

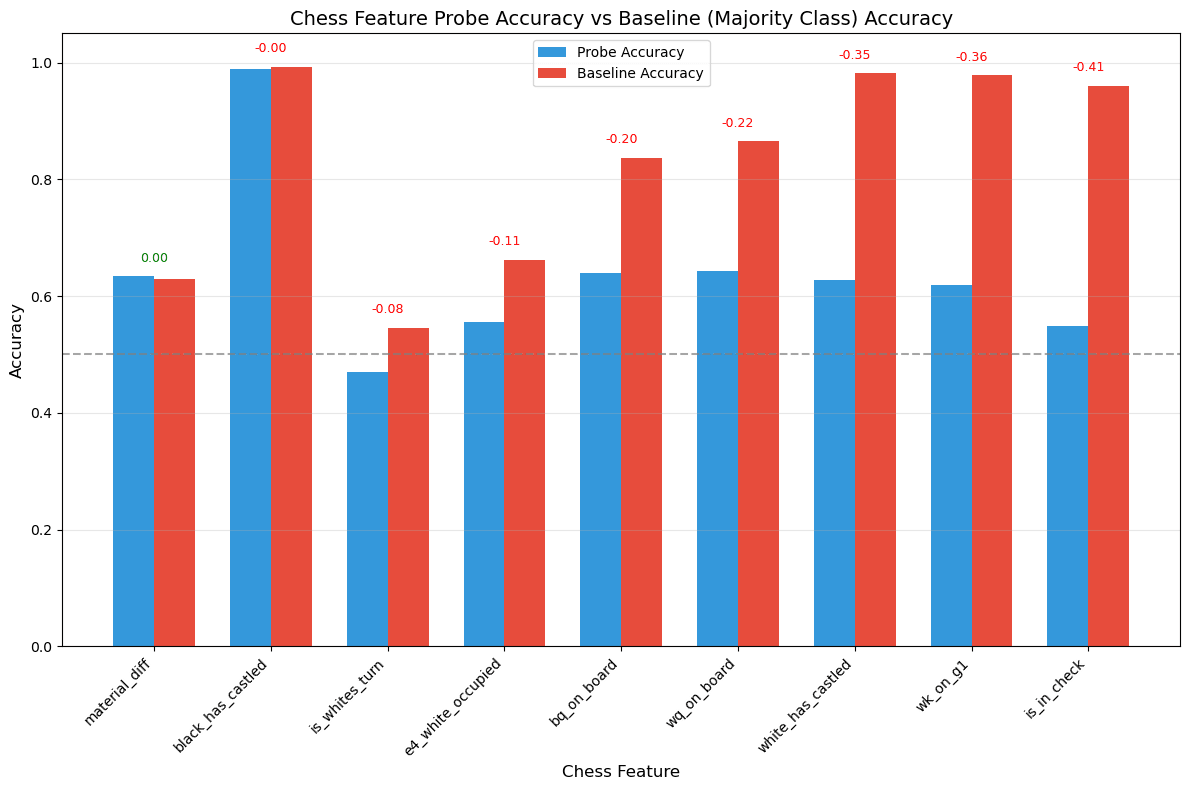
Results:

Accuracy no better than majority class baseline across all featuresNo evidence of internal board state representation

As we can see, SONAR lacks semantic chess understanding. It may recognize some syntactic patterns but doesn't maintain meaningful game state representations.

Discussion

We observe a clear hierarchy of correctness understanding in SONAR:

Code validity (strongest): 96% accuracy, clean separationLanguage grammaticality: 93% accuracy, cross-lingual robustnessBasic arithmetic: 76% accuracy, limited to additionChess legality: Weak, context-dependent signalChess semantics: Absent above baseline

Emergence from Compression Efficiency

For code and language, our explanation centers on compression efficiency. Valid patterns follow regular structures that are inherently more compressible than random sequences (think Kolmogorov complexity). The autoencoder develops an "agent overhang", i.e. correctness understanding emerges naturally from the reconstruction task rather than explicit training.

Decoders implicitly learn correctness because it improves reconstruction accuracy. If you know something follows grammatical rules or valid code syntax, you have powerful constraints that make decoding easier.

Training Data Dependency

The hierarchy likely reflects training corpus composition:

Code and natural language: Heavily present in training dataBasic arithmetic: Less frequent, explaining weaker signalsChess notation: Rare, especially random game sequences never seen during training

This suggests the model's correctness understanding is fundamentally tied to pattern frequency rather than abstract reasoning capability.

Limitations

With only one week, we limited ourselves to two analysis methods. Absence of evidence isn't evidence of absence. Different probing techniques might reveal hidden chess representations or other correctness signals.Our notion of chess "understanding" may differ from the model's internal representations. A non-linear board state encoding could exist that our linear probes can't detect.We didn't explore other correctness domains like logical reasoning, factual accuracy, or causal relationships.Linear probes can sometimes find spurious patterns. More sophisticated analysis would strengthen these conclusions.

Conclusion

SONAR autoencoders develop varying degrees of internal correctness representations, with strongest signals in code validity and language grammaticality. This pattern suggests correctness information emerges as a byproduct of efficient encoding-decoding rather than explicit training for correctness detection.

Practical Implications:

Autoencoder representations contain exploitable correctness signalsHierarchy reflects compression efficiency rather than reasoning depthCross-lingual grammaticality suggests universal syntactic encodingPotential applications in automated correctness detection tasks

Future Directions:

Non-linear probing methods for chess and other domainsInvestigation of logical reasoning capabilitiesAnalysis of factual correctness representationsComparison across different autoencoder architectures

The key insight: correctness understanding in language models may be less about sophisticated reasoning and more about the fundamental mathematics of compression. Valid structures are easier to encode, decode, and reconstruct. This makes correctness a natural emergent property of the autoencoding objective.

Discuss