本文探讨了从预训练语言模型（如 ModernBERT-large）的输入嵌入空间梯度中提取有意义信息和行为的可能性。通过计算输入嵌入的梯度，作者尝试优化这些嵌入以预测目标标记，并研究了在“马”和“狗”等具体案例中的表现。实验结果表明，虽然梯度下降可以使损失收敛，但优化后的嵌入往往难以解释，且距离原始嵌入较近。文章还提出了关于过参数化机制的假设，并进行了验证，为进一步研究提供了方向。

🔍通过计算输入嵌入的梯度，可以了解模型如何调整输入以最小化预测分布与目标分布之间的差异。

🐎在“动物叫声”的案例研究中，梯度下降尝试将“bark”优化到“neigh”，结果显示虽然损失收敛，但嵌入向量的移动距离有限，且难以改变其原始含义。

🤔作者认为，对输入嵌入空间的梯度下降可能处于“过参数化状态”，这意味着全局最小值的集合是广泛且相互连接的，导致结果难以解释。

✅通过随机初始化输入嵌入并进行梯度下降，实验验证了“过参数化状态”的假设，结果表明即使初始状态随机，模型仍能收敛，且嵌入向量的移动距离有限。

💡文章探讨了多种正则化方法，例如 L1 正则化和惩罚注意力层的高熵等，但并未取得显著成果，但惩罚注意力层的高熵是一个值得关注的方向。

Published on June 24, 2025 8:24 PM GMT

This is the first in a series of posts on the question:

"Can we extract meaningful information or interesting behavior from gradients on 'input embedding space'?"

I'm defining 'input embedding space' as the token embeddings prior to positional encoding.

The basic procedure for obtaining input space gradients is as follows:

Transform tokens into input embeddings (but do not apply positional embedding).Run an ordinary forward pass on the input embeddings to obtain a predicted token distribution.Measure cross-entropy of the predicted distribution with a target token distribution.Use autograd to calculate gradients on the input embeddings with respect to cross entropy.

The result is a tensor of the same shape as the input embeddings that points in the direction of minimizing the difference between the predicted and target distribution.

Implementation

These experiments were performed with HuggingFace's transformers library and the ModernBERT-large model (Dec 2024).

ModernBERT-large was chosen because:

Despite being "large" it is lightweight enough for rapid experimentation.It has a strong and ready-made visualization suiteBidirectional encoders are easy to reason about.The mask in-filling capabilities were attractive for experimentation purposes (for example: ablation studies).

I used HuggingFace's transformers because it allowed for fairly low level access to model internals - which was quite necessary as we will see.

Obtaining input embeddings prior to positional embeddings was a little tricky but no means impossible:

tokenizer = AutoTokenizer.from_pretrained(MODEL)model = AutoModelForMaskedLM.from_pretrained(MODEL)tokenized = tokenizer(sentences, return_tensors="pt", padding=True)inputs_embeds = model.model.embeddings.tok_embeddings(tokenized['input_ids'])

Luckily for us, we can pass input_embeds directly into the model's forward pass with a little bit of surgery, and this works out of the box.

    tokenized_no_input_ids = {         key: value         for (key,value) in tokenized.items()         if key != "input_ids"    }    model_result = model(**tokenized_no_input_ids,       inputs_embeds=inputs_embeds)

Finally, we can use torch's built-in autograd capabilities to get our input space embedding:

    inputs_embeds_grad = torch.autograd.grad(        outputs=loss,        inputs=inputs_embeds,        create_graph=False,        retain_graph=False,        allow_unused=False        )

Case Study: Horses and Dogs, Neighs and Barks

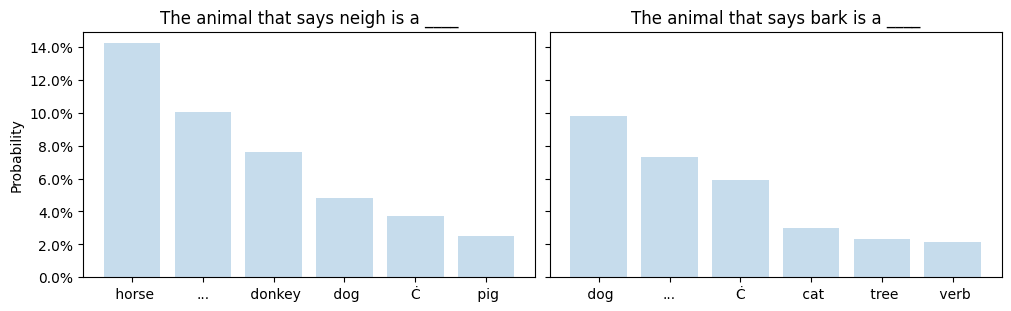
To make things more concrete, let's start with two prompts:

"The animal that says bark is a ""The animal that says neigh is a "

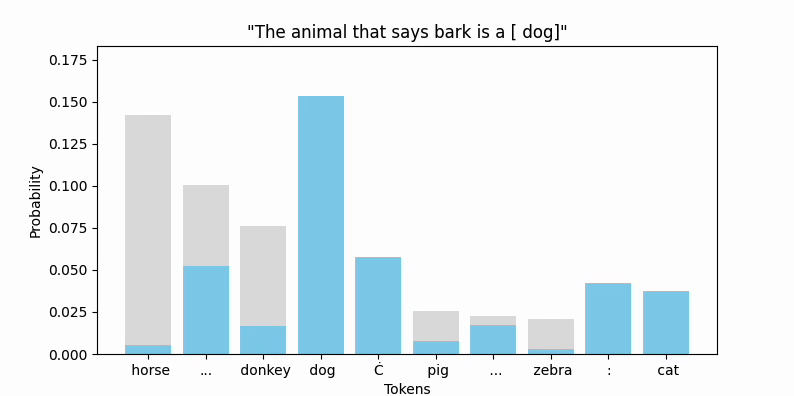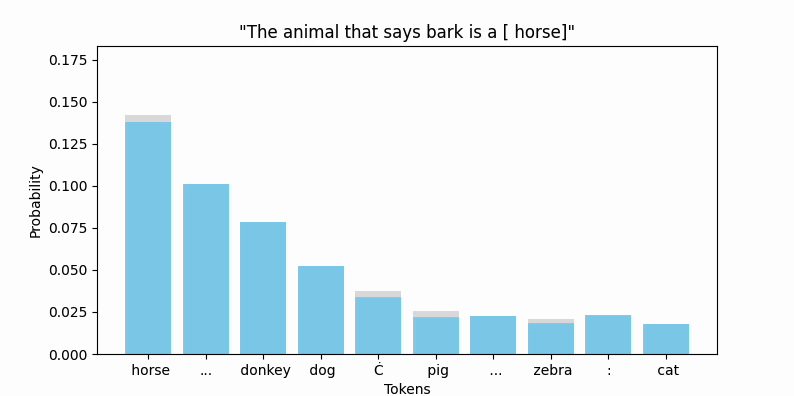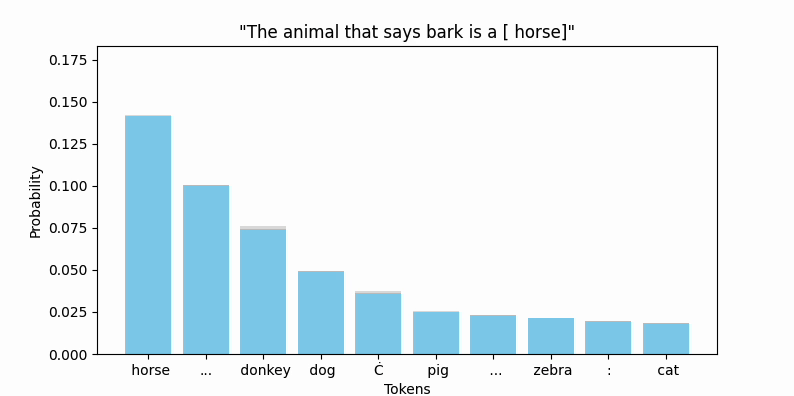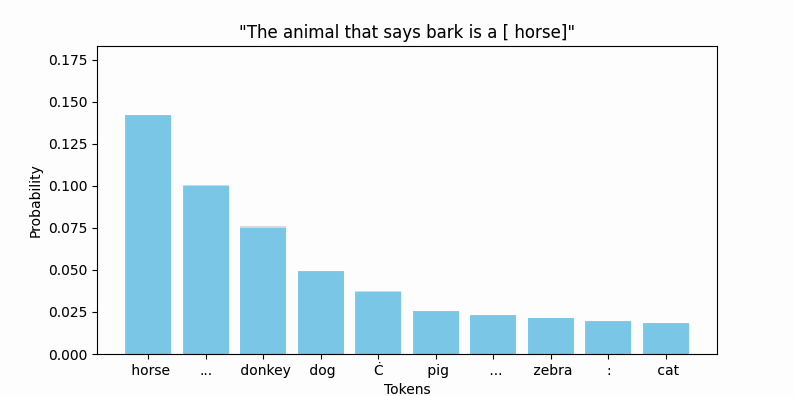
The token distributions as predicted by ModernBERT-large are, respectively:

Representing the left distribution as 🐶 and the right distribution as 🐴, we are computing the gradient of:

with respect to cross_entropy(🐶,🐴).

Which means:

"Figure out which direction each token wants to go in order to fill in the blank with 'horse' instead of 'dog'".

As a gut-check, let's measure the L2 norm of the gradients for each token to give us a rough sense of the "impulse" given by cross entropy on each token:

The tokens with the top 3 gradient L2 norms are "says", "dog" and "animal".

This is encouraging. But are the gradient directions meaningful?

Let's see if any of the gradients point in a neigh-like direction by finding the vocab token with the largest cosine similarity to our gradient: argmax(cosine_sim(gradient, vocabulary))

However, perhaps this is the wrong question to ask. We want to understand if the gradient is heading towards any vocab token starting from the initial embedding:

argmax(vocab, cosine_sim(gradient, vocab - bark))

Sadly, this yields the same set of tokens because the gradient vectors are mostly orthogonal to the original embedding (indeed, they all have a cosine similarity of about -0.01):

ADAM on Input Embeddings

Although the early indications are mixed, it would be interesting to try to ADAM optimize the input embeddings.

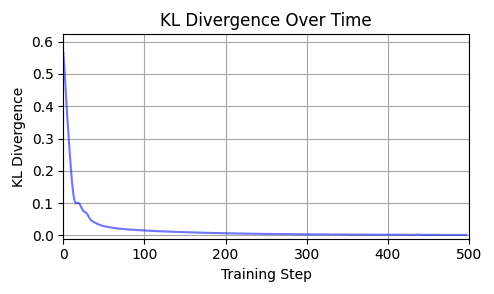
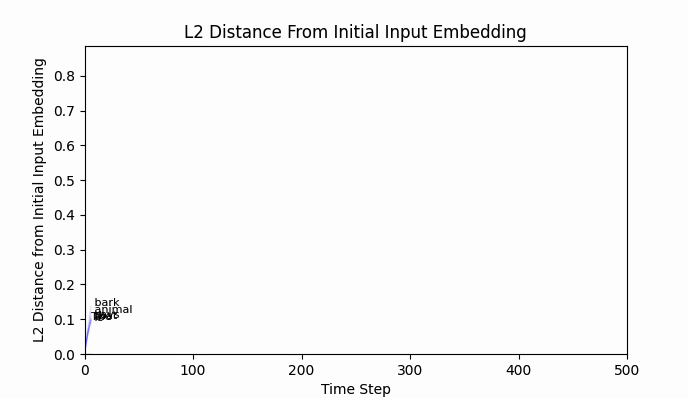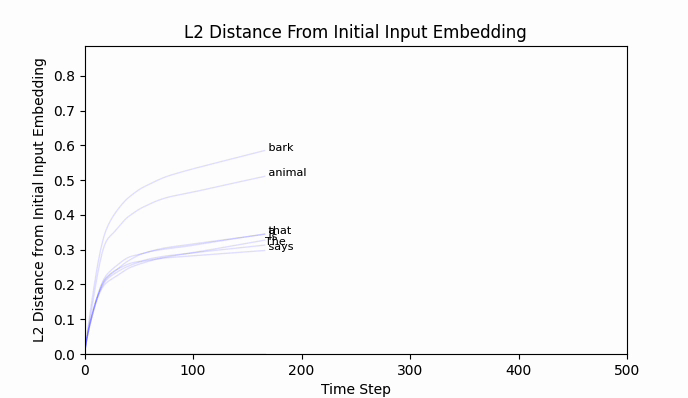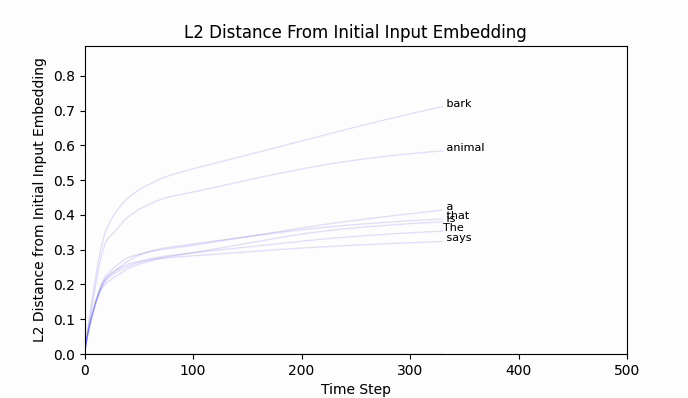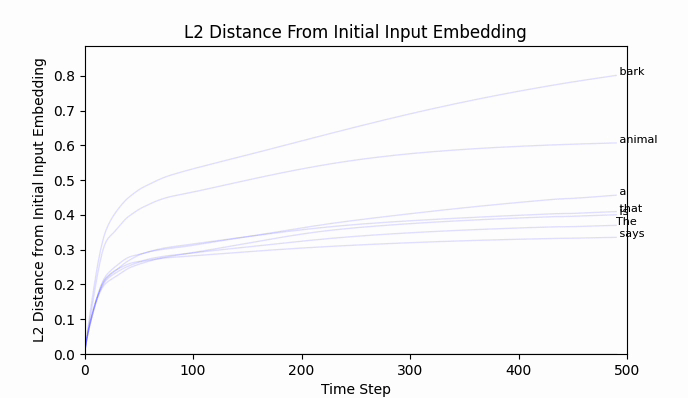
It does converge (quite rapidly):

Animating the top token probabilities illustrates the convergence quite nicely:

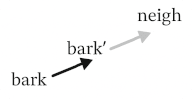
And most encouragingly, " bark" seems to be on the move!

While " bark" is moving, I should point out that the new embedding (we can call it bark'), is still firmly in " bark" territory. No other vocab token is closer by cosine similarity or euclidean distance.

The Euclidean distance between " neigh" and " bark" is around 2.5, and after 500 training steps we have barely traveled 0.8. An extended training run of 10,000 steps still lands bark' firmly in bark world.

But has " bark" traveled towards anything in particular?

Indeed - "bark" has traveled more towards neigh than any other token in the vocabulary.

While this is encouraging, the cosine similarity of the heading towards neigh is nothing astonishing: about 0.3.

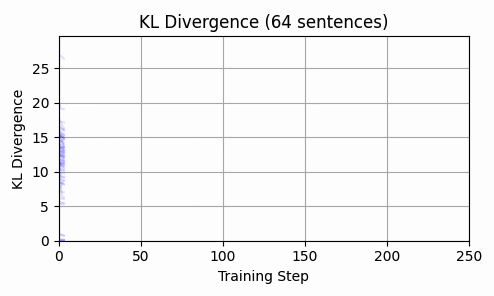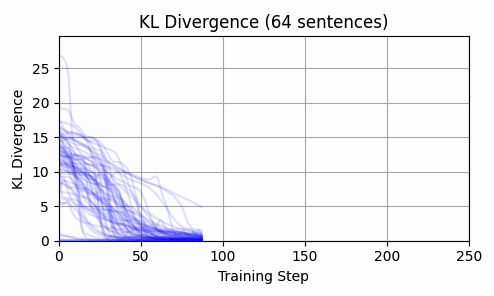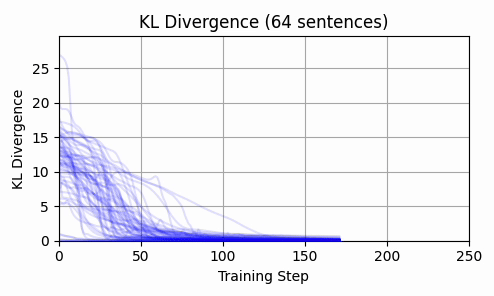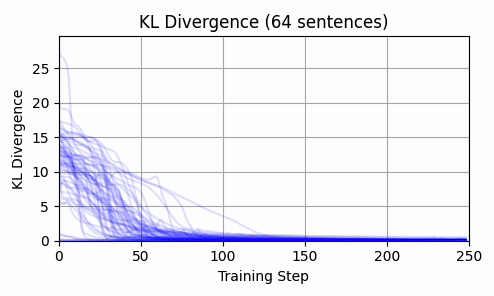
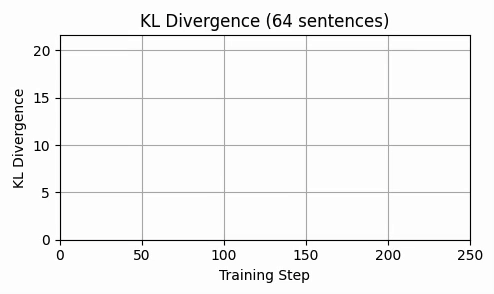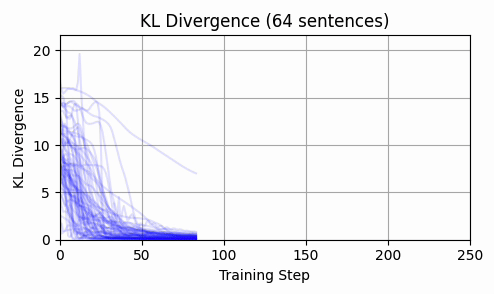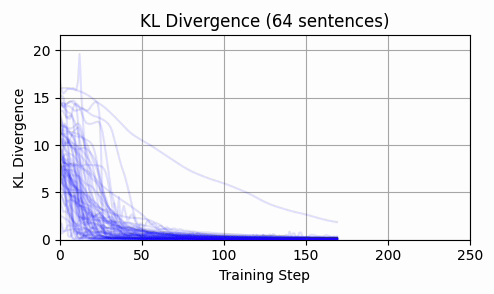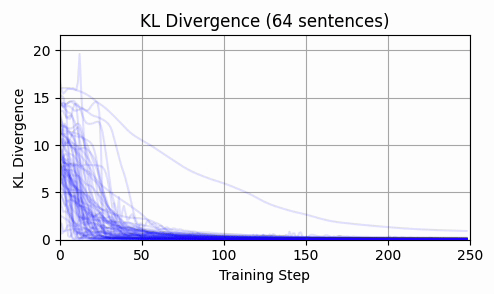
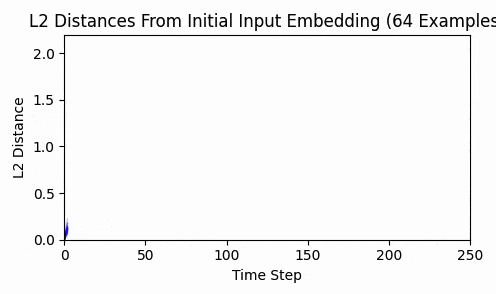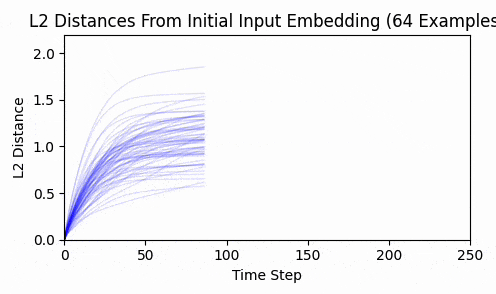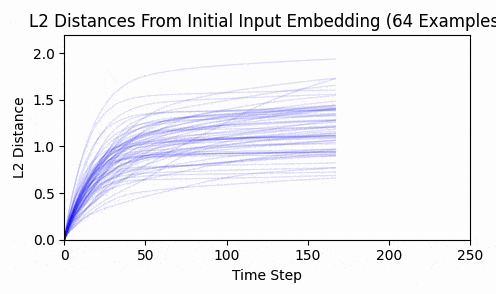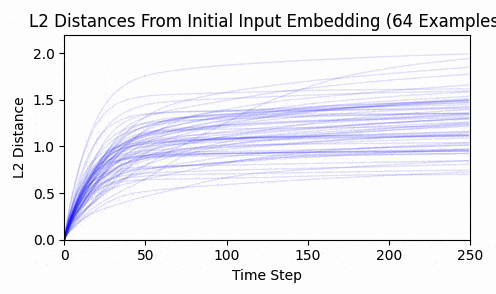
Repeating this exercise over 64 examples, we can see that 'bark' is a bit of an outlier (it was a contrived example). The total L2 token embedding distances per sequence typically level off, while the KL-divergence approaches zero.

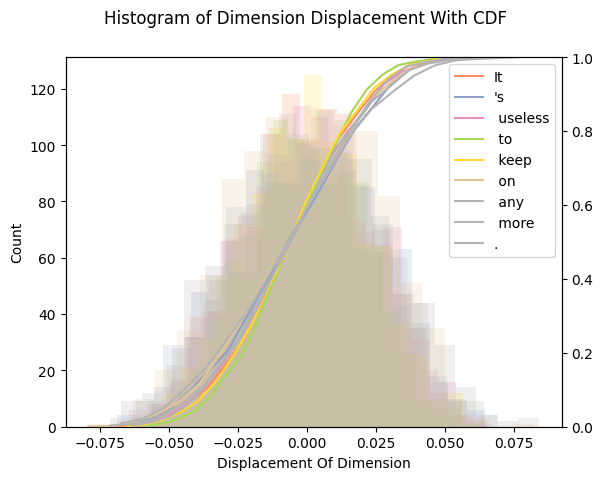
Is there any kind of structure about which dimensions are affected? By inspecting a histograms and cumulative density plots of per-dimension movement in input embedding space, it doesn't appear that any particular token was "favored" - all tokens had a roughly equal distribution of embedding dimension displacement. The following histogram from our 64 test examples is typical.

Some Hypotheses

I conjecture that performing gradient descent on input space embeddings is in the "overparameterized regime".

This has some implications for where and how we minimize to nearly zero loss.

Specifically:

The global minima manifold is "close to everywhere".There are almost no local minima - which means that the global minima is reachable from every starting point by gradient descent.The "global minima manifold" is conjectured to be vast and interconnected.

The first point is uncontroversial - it is a well known property of high dimensional Euclidean space that all points become "close".

The second point helps explain why loss in the overparameterized regime almost always converges to nearly zero.

The third point explains why we should have no expectation that the point we converge to is in any way interpretable: The global minima manifold is itself quite high dimensional, and only a tiny fraction of the points on it have sensible back-projections.

TLDR; our consistent ability to converge to zero loss, the lack of interpretability of the results, and the relatively short distance our embeddings travel all lend support to the claim that we are seeing a classic loss landscape.

More Validation - Randomized Input Embeddings

But, to further validate our hypotheses about a vast and everywhere-close global minima manifold, we will conduct a final experiment:

Prior to gradient descent, replace the input embeddings with a random point sampled from a hyper-ellipse fitted to the ModernBERT-large input embeddings.Run gradient descent as usual.Inspect loss for convergence and input embedding L2 distances per sequence.

If loss converges and we again observe that the input embeddings do not move "very far" and "level off", this is good evidence for our hypothesis.

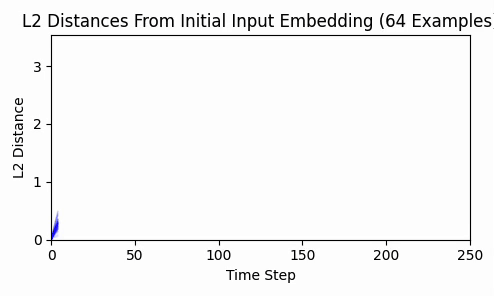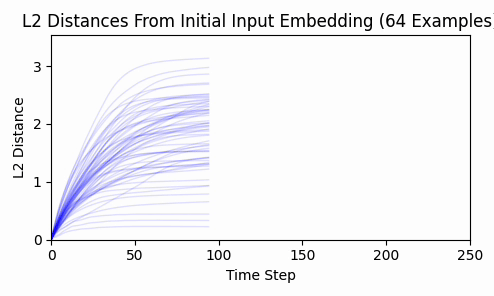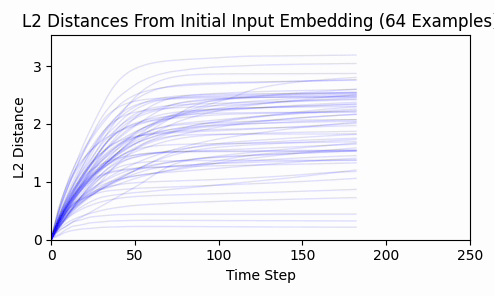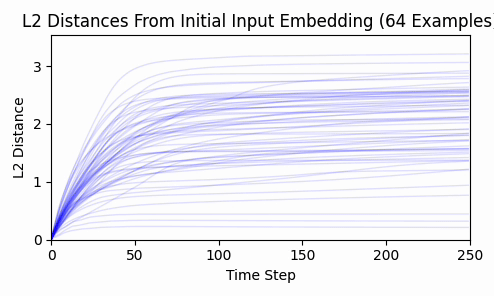
Here are the results:

Again - we consistently converge, and not a single token moved enough to back-project to a new token.

This is strong evidence in my opinion that input embeddings is in the overparameterized regime.

Next Steps

Some other directions I have explored include:

L1-Regularizing the input embeddings.Penalizing high entropy in the attention layers (under the hypothesis that ADAM optimizing input embeddings leads to "shotgun approach" in the attention layers.Penalizing soft minimum of distance from the nearest token in the vocab.

None of these were particularly successful at "guiding" input space embeddings towards interpretable results.

However - penalizing high entropy on the attention layers not only converged but is an extremely interesting idea that I will explore in my next post.

Discuss